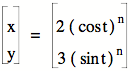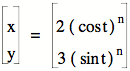Department of Mathematics and Science Education

 

 

 

 

 

Allyson Hallman

 

 

 

 

 

A Very Unexciting Exploration of Parametric Equations

 

 

 

 

Consider: x = a cos t    for three fairly obvious cases.

                 y = b sin t

 

 

 

 

Case #1:

 

 

 

 

 

 

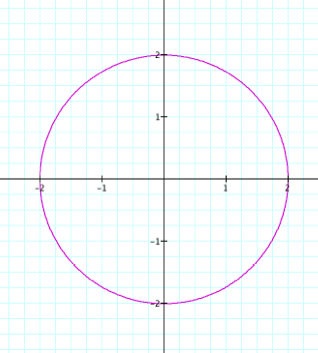
Pictured we have

 

 

 x = 2 cos t

 y = 2 sin t

 

We have generated a circle centered at the origin with radius 2.

 

Click here to view Clip where a and b vary from -5 to 5. 

These graphs are symmetric about both the x- and y-axis. A negative a value reflects over the y-axis and a negative b value reflects over the x-axis. But due to the symmetry of these graphs these negative values have no effect on the graphs generated. And so we consider the absolute value of a and b without loss of generality.

 

 

 

 

Case #2:

 

 

 

 

 

 

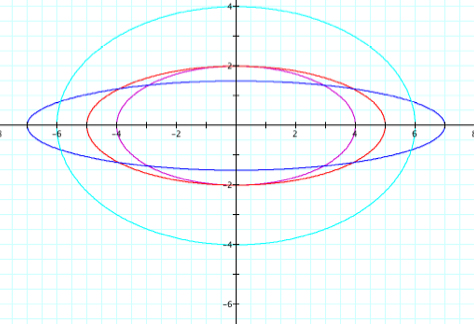
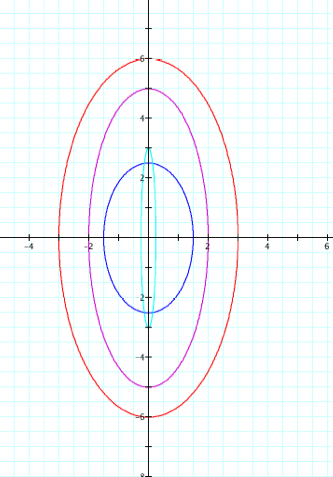
WhatÕs going on? Looks like fun with ellipses.

 

So we have ellipses centered at the origin and with major axis of length  along the x-axis and with minor axis of length along the y-axis

 

 

 

 

 

 

Case #2:

 

 

 

 

 

 

 

Still ellipses. (whoop-tee-doo)

So we have ellipses centered at the origin and with minor axis of length  along the x-axis and with major axis of length along the y-axis

 

Ok, what happens if square stuff?

 

 

 

 

Consider: x = a (cos t)2   

                 y = b (sin t)2

 

 

 

 

 

Case #1:

 

 

 

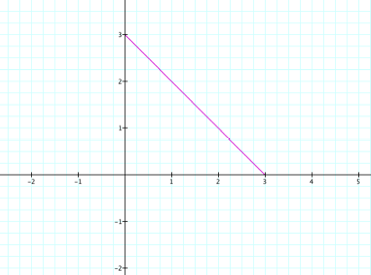
Pictured we have

 

 

 x = 3 (cos t)2

 y = 3 (sin t)2

 

We have generated a line with slope -1 and y-intercept of 3.

 

Click here to view Clip where a and b vary from -5 to 5.

 

 

 

 

Case #2:

 

 

 

 

 

 

 

 

 

 

 

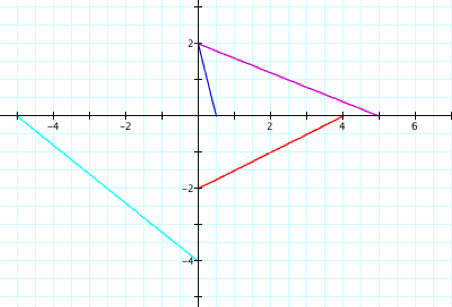
OH FUN. A bunch of lines. What does it all mean?

 

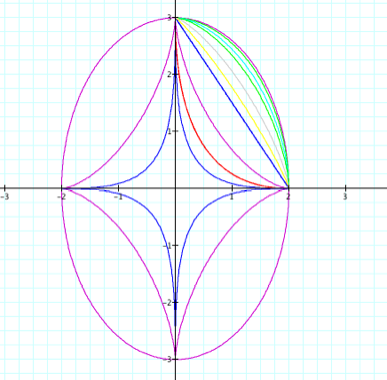
The slope of the line is equal to  , the y-intercept is b, and the x-intercept is a.

 

 

 

 

Consider: x = a (cos t)3

                 y = b (sin t)3

 

 

 

 

 

 

 

 

 

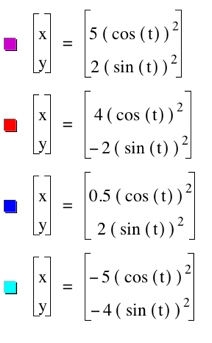
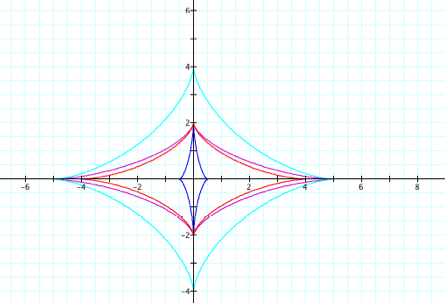
Ok, well this is much less boring than what we had before.

 

Our lines are curvy, forming these cool diamond like things that are symmetrical over the x- and y-axis.

 

x-intercepts are (-a, 0) and (a, 0) and our y-intercepts are (0, -b) and (0, b).

 

 

 

 

I wonder what happens if increase the exponent more.

 

 

 

 

 

 

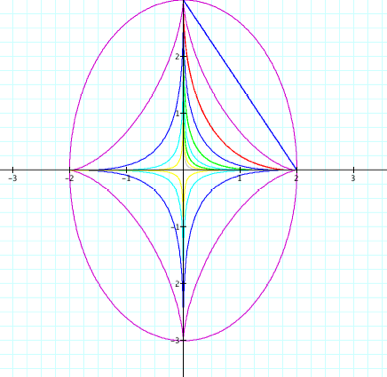
Values of n take on integers from 1 to 10.

 

As the exponents decrease from 10 to 2, we are approaching our straight line. Then we jump from the straight line out to the ellipse which had an exponent of 1.

 

I wonder if we examine exponent values between 1 and 2 if we will fill in the space between the straight line and the ellipse

 

 

 

 

 

Ha, we have some additional values of n = 1.05, 1.15, 1.25, 1.5, 1.75

 

And lo and behold they fall within the space between the straight line and the ellipse.

 

Super, I am glad this one finally got a bit more interesting.

 

 

 

 

Not to thrilled with this assignment? (yea, me neither) Go home.