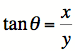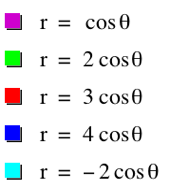Department of Mathematics and Science Education

Allyson Hallman

Exploration of Polar Equations

Brief reminder:

Our variables are r and q, where q represents our angle with initial side formed by the positive x-axis, and r represent the distance traveled away from the origin along the terminal side of the angle. Translating between polar coordinates and rectangular coordinates requires the following set of equations:

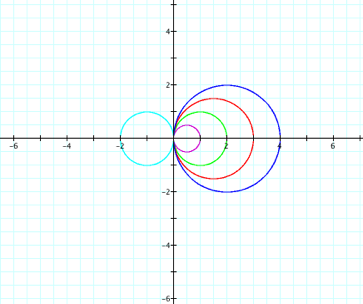
Consider r = acos q

We have circles centered along the x-axis with diameter equal to a so the radius must be . (that’s probably why Dr. Wilson told us to look at 2a. whoops.) So the center is and the radius is

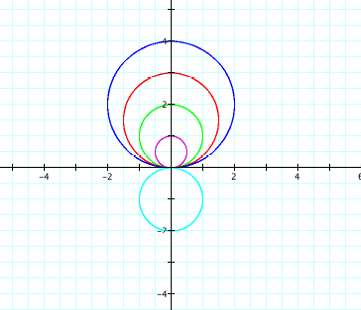
Consider r = asin q

We have circles along the y-axis with center with diameter equal to a so the radius must be .

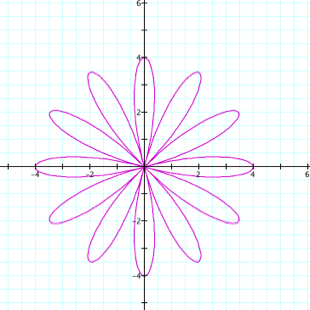
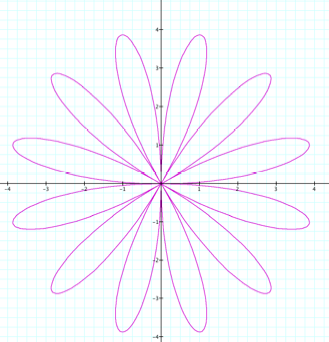
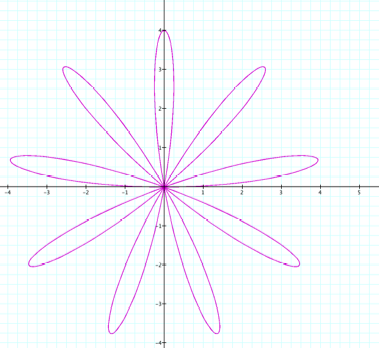
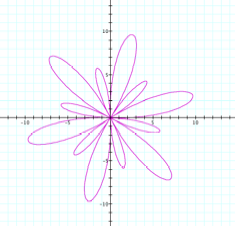
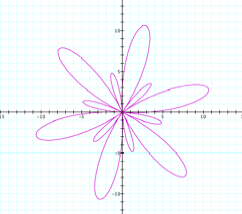
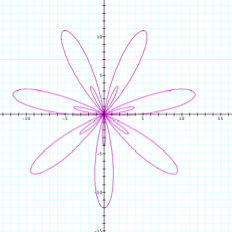
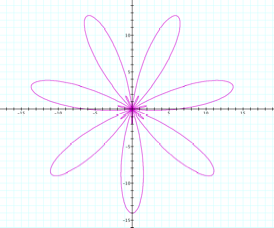
Consider r = 4cos kq

r = 4cos kq, where k is even

r = 4cos kq, where k is even

Pretty flowers, called roses. We distinguish them by the number of leaves they have (although I really think since it’s a rose we should call them petals.) First we notice that our a value 4 now gives us the radius of the rose, where as before when dealing with circles, a was the diameter. (I just picked 4 to get a nice large picture in graph, now it dawns on me I could have just changed the scale an gotten the same effect. Oh well.) Secondly, and far more cool and interesting, notice that when k is even we have 2k leaves and when k is odd we have k leaves. Does the same hold true for sine?

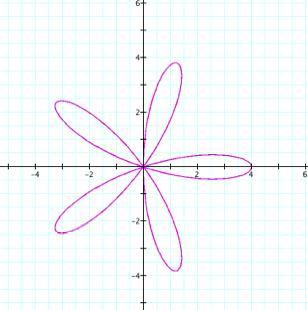
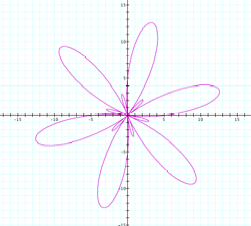
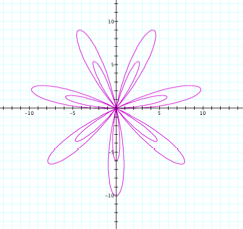
r = 4sin kq, where k is even r = 4sin 6q,

r = 4sin kq, where k is odd r = 4sin 9q,

Click here to explore for other even values of k and odd values of k in graphing calculator. (I advise against just hitting play as it will run to fast to be of use. I suggest clicking on the slider and moving it with your mouse the two graphs are set up to display only even or only odd values of k.

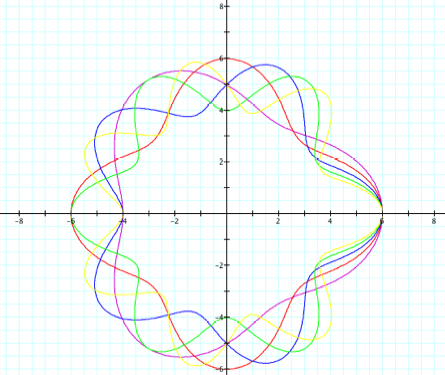
Consider r = acos (kq) + b. Turns out there’s a lot going on here and so we’ll begin by just letting a = 1, and after we establish some stuff, we’ll move on to examining for different values of a. We begin with r = cos (kq) + b.

Things to take note of: Our k value still represents the number of leaves, however, now the leaves don’t actually close so we are going to call them “waves.” In our previous example the number of leaves was dependant on the parity of k (k leaves if k is odd, 2k leaves if k is even). In this scenario, parity no longer has an effect; the value of k is equal to the number of “waves.” But what affect will the b value have? The b value will determine the height of each wave. The minimum of each wave is 4 units from the origin and the maximum of each wave is the 6 units from the origin and the average of 4 and 6 is in fact 5, our b value. (We’re going to find a more sophisticated way to talk about this shortly, hand in there.) Does that always work? Let’s Try for a different value of b.

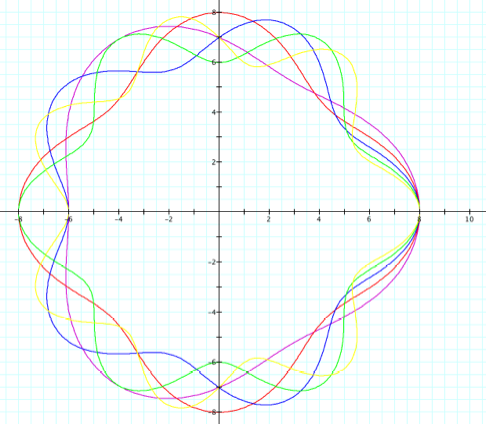
Now with a b value of 7, we expect the average of the minimum and maximum distance of our graph from the origin to be 7. The minimum of each wave is 6 units from the origin and the maximum of each wave is the 8 units from the origin and the average of 8 and 6 is in fact 7, our b value. Fabulous. However, (you knew it was coming) there are other pairs of numbers that have an average of 7. Will it always be the case that the maximum and minimum distance of the curve fromteh origin will always be b + 1 and b – 1, respectively? Hmm… Lets start varying the a value and see what happens.

We have six loops as expected form the 6q. We can clearly see the maximum and minimum distance from our curve to the original is not 7 + 1 = 8 and 7 – 1 = 6. Consider the yellow graph of r = 6cos 6q + 7. The maximum distance form the origin is 13 and minimum distance 1. So then our 7 + 6 gives the maximum and 7 – 6 gives our minimum and by the way the average of those two is still 7. So the maximum distance from the curve to the origin is and the minimum distance is , which also still works out fine when b = 0 in which case the length of the petals (or radius of the flower) is a. However, when b = 0 and k is even we also get 2k leaves and we haven’t accounted for that yet. In this scenario, regardless of the parity of k we have k leaves. Hmm….

In both cases above, we have b > a. Suppose that a > b. This time for fun, we’ll look at sine.

Long leaf = Short leaf =

Long leaf = Short leaf =

Long leaf = Short leaf =

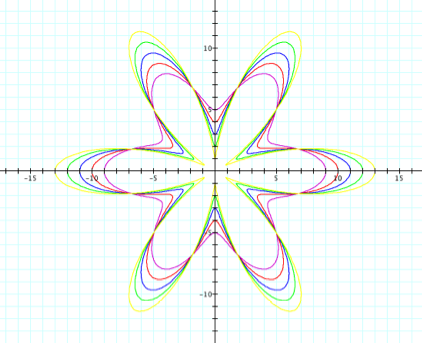
Ok, now we can see that if b > a we will get double leaves where is the length of the longer leaf and is the length of the shorter leaf. Hey, this accounts for the double leaves when b = 0 and k is even. If b is 0 and k is even then we double the number of leaves to 2k and both sets of leaves will have length a.

Above, we have examined the case where b > a and k is even. What about when b > a and k is odd? Remember that when k is odd we should only have k leaves, but if b > a, we should get a second set of k leaves. Oh dear. Let’s examine the case where b > a and k is odd

As before, we have 2k leaves and:

Long leaf = Short leaf =

Long leaf = Short leaf =

Long leaf = Short leaf =

Ah ha! If k is odd the 2^nd set of leaves occur within each leaf of the original set. So when b = 0 shorter set will lie exactly on top of the original set producing a graph with k leaves with length a!!! Meanwhile if k is even, the 2^nd set of leaves occurs with one in between each of the original set of leaves and so when b = 0 the graph produces 2k leaves of length a.

Go home.