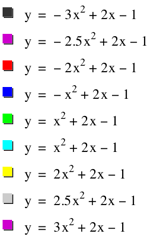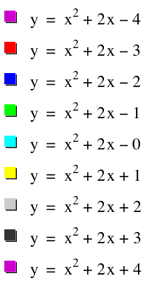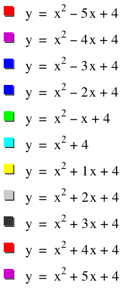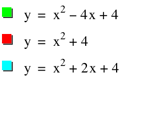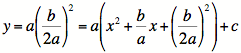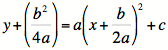Department of Mathematics and Science Education
	Allyson Hallman
Explorations with Quadratics
Consider y = ax^2 + bx + c
Part I: ‘a’ varies
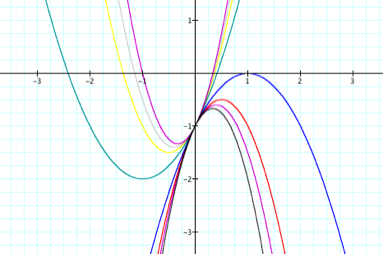
What happens? Two things should be jumping out a you 1) Equations with negative values for a produce graphs that open down and equations with a positive values for a produce graphs that open up. 2) As the absolute value of a gets larger our graphs become more narrow (they shoot towards positive or negative infinity faster). This is more interesting than it might appear. If you consider the second derivative of any quadratic it will be the a value. The second derivative represents acceleration, so the larger the a value the faster the increase of velocity and accordingly a quicker progression towards positive or negative infinity. Check this out in graphing calculator, press play to vary the value of a from -20 to 20. Notice that when the value of a approaches zero, the approximates a line, and of course when a is 0 we have the line y = 2x – 1.
Part II: ‘c’, the constant term varies
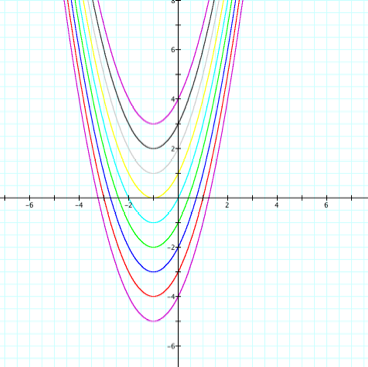
What happens? If this was really surprising to you, you clearly were not paying attention when we covered transformations of functions. (shame on you.) Remember that f(x) + c shifts our vertically c spaces. (if c > 0, shift up and if c < 0, shift down.) So the actual parent graph in this case is y = x^2 + 2x. Notice also that c is having some affect on the number of real roots we have. A quick with glance without thinking might lead you to believe that c > 0 produces no real roots, c < 0 produces two distinct real roots, and c = 0 produces one real (repeated) root or two roots that aren’t distinct. But we can see from our graph that this is not case. We’ll come back to the “root issue” later.
Part III: ‘b’, the constant term varies
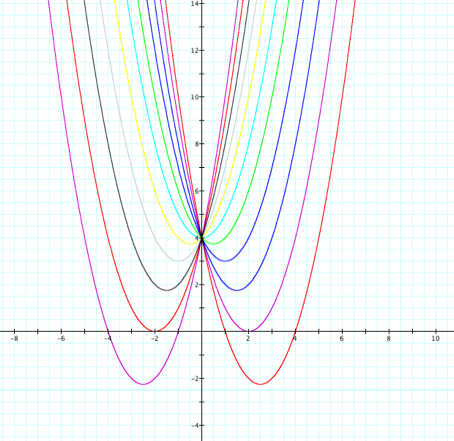
Well, gosh it sure is pretty, but what does it all mean? The graphs appear to be moving up and down and left and right. We must have done something wrong. When we investigated c, we discovered as c varied, our graph shifted vertically. However, here the value of c is held constant at 4 but our graph is still shifting vertically. Actually everything is as it should be. In our previous investigation c was being added to the same graph, y = x^2 + 2x, whereas in this investigation the same c is being added different graphs because the coefficient of the linear term is changing each time. So rest assured, b is not affecting the vertical shift. But surely, all of the graphs having the same constant term of 4 will have some common affect. Speaking of common, what do all of the graphs pictured have in common? That’s right the y-intercept of 4, which certainly makes sense. Evaluating those (or any) quadratic functions for 0 will always result in our constant term. And so c represents not only the vertical shift of the parent function but also the y-intercept of the parabola. So the only remaining interesting thing happening is the horizontal shift, which is surely caused by b. One might suppose that a coefficient of -4 for the linear term of the quadratic would produce a horizontal shift in the parabola of 4 units left. From our examples above, we can see that this is not the case. Remember again from our knowledge of transformations, that f(x + h) produces horizontal shifts. The question then become how is coefficient of the linear term of the quadratic affecting what is added to x? Let’s examine just a few examples to see what is going on here.
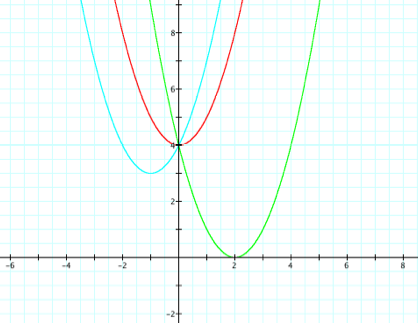
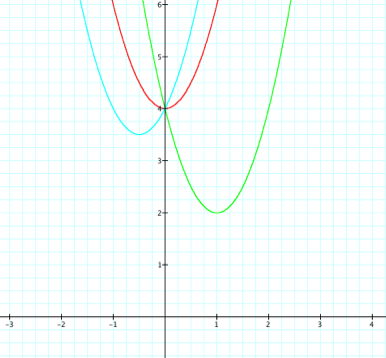
The red graph is our original. Our foolishly wrong suspicion was that adding 2x would shift 2 spaces right and subtracting 4x would shift 4 places left. We can see from examining the blue graph that in reality adding 2x shifted in 1 pace to the left and subtracting 4x shifted our graph 2 spaces right. So in fact the shift is half of what we supposed and in the opposite direction. That’s not so shocking. Remember again that f(x + h) produces horizontal shifts to the right if that h < 0 and to the left if h > 0. But why is dividing by 2? Will this always be the case? Consider the following:
Now with an a = 2, we can see that blue graph is not shifted left one space, but left 0.5 of a space, or a fourth of what we originally thought. Likewise, instead of shifting 2 spaces right our green graph is 1 space to the right. What is going on here? It seems that both a and b have affect on the horizontal shift of the graph. Let’s return to our original equation and use some algebra skills to determine what’s happening.
		Original equation Factor out a. Complete the square by adding half the linear term squared to both sides. Factoring the perfect square trinomial you just created into a binomial squared. Solving for y.
Now it is pretty easy to see that when varying all the coefficients together there is interaction among them. Both a and b contribute to the horizontal shift and a, b, and c contribute to the vertical shift. Specifically, the vertical shift is , up if this value is positive and down if its negative. The horizontal shift is , left if this value is positive and right if its negative.
What? The roots, oh yes, I did mention we’d talk about those later. Well, in reality this is something you already know. Remember the quadratic formula . What about this determines the number of roots? That’s right the discriminant, a.k.a. the junk under the radical, . If the discriminant is greater than 0, we will have 2 real distinct roots, if it’s less than 0 we will have no real roots, and if it equals zero 1 real repeated root.
Ready to go home?