Allyson Hallman

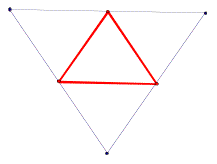
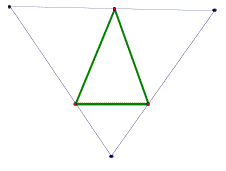
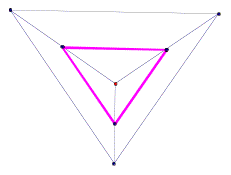
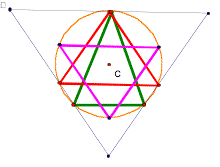
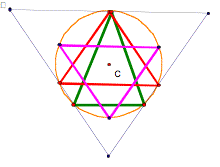
Consider the any triangle. Construct the orthic triangle, medial triangle, and the triangle whose vertices are the midpoints of the segments connecting the vertices to the orthocenter. (Need to refresh on your definitions? Check out GSP library.)
Medial Triangle is in red.		Orthic Triangle is in green.			Orthocenter-Midsegment Triangle is pink.
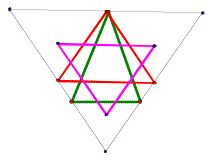
And all together we have.
If we construct the circumcircle of each of our triangles (red, green, and pink), what might we notice? Ah ha. It would appear that each of our triangles actually have the same circumcircle, and accordingly the same circumcenter. Why is this so? Want to explore the diagram in GSP? Click here						.
To fully understand the relationship between our secondary triangles, we need to further examine the idea of circumcenter. In general how do we know that the perpendicular bisectors of all three triangles are concurrent? In fact how do know that the perpendicular bisectors of one triangle are concurrent? It is here that we will begin our discussion.
Proof of concurrency of perpendicular bisectors of a triangle
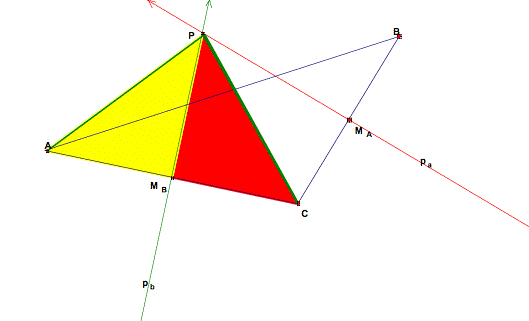
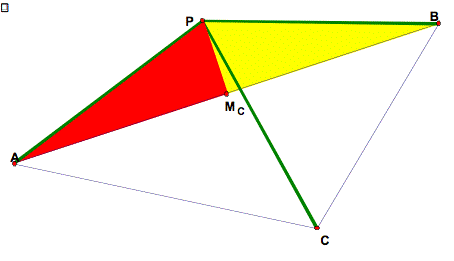
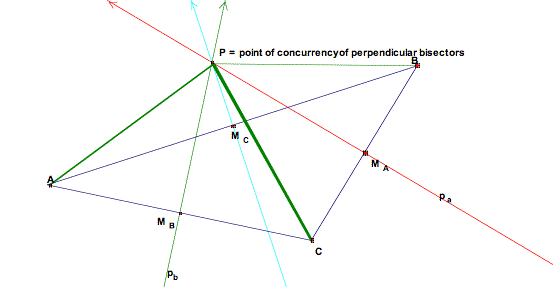
First, we will begin with any triangle, call it ΔABC. Constructing the midpoints (MA, and MB) of two sides of the triangle (sides a and b) and then each line that its perpendicular to one these sides and through its midpoint, will give us a construction of the perpendicular bisectors of two sides of the triangle. It is quite obvious that these two perpendicular lines will intersect. Because we are working in the plane, lines pa and pb are either parallel or intersecting. The only scenarios in which lines pa and pb would be parallel is if they were perpendicular two a pair of parallel sides or if they were perpendicular to two sides contained in the same line. Clearly, in any triangle, it is impossible for any two sides to be parallel. If any two sides are contained in the same line, then we are looking at a degenerate triangle (where all segments are contained in the same line), but for our purposes we are only considering non-degenerate triangles. Now, that we are convinced that our two perpendicular bisectors, pa and pb, interest, let us call their point of intersection, P. It then remains for us to show that the perpendicular bisector of the third side of our triangle also contains point P.
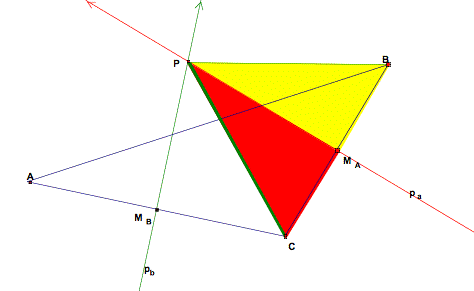
We now want to show that : (Yellow is congruent to Red.) because the midpoint of a segment divides it into two congruent segments. because the lines AC and pb perpendicular at point MB form two congruent right angles. because congruence is reflexive. And so we have shown by the Side-Angle-Side Congruence Postulate for Triangles. because corresponding parts of congruent triangles are congruent.
We now want to show that : (Yellow is congruent to Red.) because the midpoint of a segment divides it into two congruent segments. because the lines BC and pa perpendicular at point MB form two congruent right angles. because congruence is reflexive. And so we have shown by the Side-Angle-Side Congruence Postulate for Triangles. because corresponding parts of congruent triangles are congruent.
“So what?” you may be thinking. How do these pairs of congruent triangles help us? Let’s see. We have shown that and . So we can conclude that because congruency is transitive. (All three green segments are congruent.) If only we can show that point P is on the perpendicular bisector of side c, we would have shown that all three perpendicular bisectors are concurrent. Let’s consider some more congruent triangles.
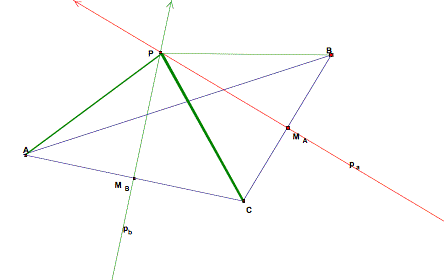
Now, let us construct the midpoint of side c of the triangle, Mc and then attempt to show that . (Again, Red is congruent to Yellow.) because the midpoint of a segment divides it into two congruent segments. which we determined from the examining the two previous pairs of congruent triangles. (remember we said all three green segments were congruent?) because congruence is reflexive. And so we have shown by the Side-Side-Side Congruence Postulate for Triangles. because corresponding parts of congruent triangles are congruent. From the angle addition postulate, we know that , which in turn tells us that and are supplementary angles. If two angles are supplementary and congruent, then they must be right angles. Because segments AB and PMc form right angles at Mc, we can conclude that they are perpendicular at Mc. The line containing segment PMc is thus the perpendicular bisector of side c of our triangle (it is perpendicular to side c and contains the midpoint of side c and that meets the conditions set by the definition of perpendicular bisector.)				Note: Our perpendicular bisectors, pa and pb, were removed temporarily with the intended purpose of simplifying our diagram.
And, that, at long last does it. We have shown that the perpendicular bisectors of the three sides of our triangle meet at point P. Hey, could they meet at any other point? No, if they did, that would violate an axiom of Euclidean Geometry, that two distinct intersect in exactly one point. So, (drum-roll please) the perpendicular bisectors of a triangle are concurrent. Along the way we actually showed that the point of concurrency is equidistant from the vertices of our triangle (yes, the green segments are congruent.)
				Remember this fun guy way back at the beginning? We were trying to determine why his medial, orthic, and orthocenter-midsegment triangle had the same circumcircle. I foolishly thought that I might need to show each of those three triangles’ perpendicular bisectors were concurrent at the same point and then that that point was equidistant to the three vertices of triangle. Silly me. The nine points generated by these three triangles are in fact the nine points of the original triangle that lie on the nine-point circle. Thus the nine-point circle circumscribes each of these three triangles and so it is the circumcircle of the three triangles.