|
|
|||
|
Department of Mathematics and Science Education |
|||
|
|
|
|
|
|
Allyson Hallman |
|||
|
|
|
|
|
|
Exploration of Tangent Circles |
|||
|
|
|
|
|
|
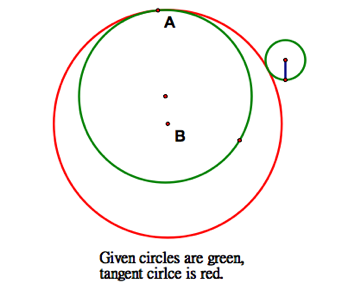
Given two circles, can we construct a circle tangent to both? Sure, here’s the tool. |
|||
|
|
|||
|
We actually have several cases to explore. |
|||
|
|
|
|
|
|
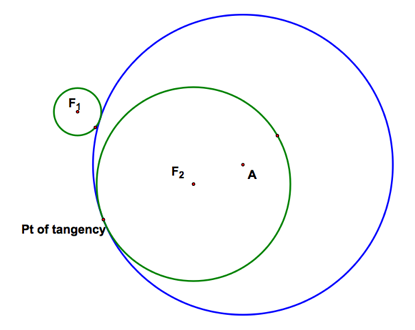
Case #1: One circle is entirely contained within the other |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
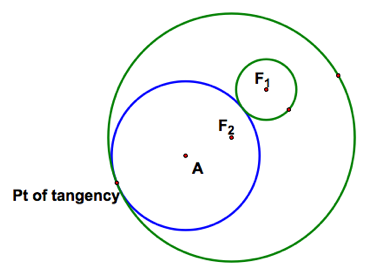
What is the locus of the center of the tangent circle? |
|||
|
|
Hey the locus looks like an ellipse… Are we sure? If it is an ellipse, then the sum of the distances from any point to the two foci is constant. Click here to explore tutorial in GSP. And in fact the sum of the distances is constant. |
||
|
|
|
|
|
|
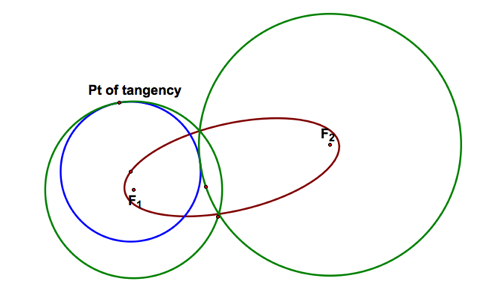
Case #2: The original circles are intersecting. |
|||
|
|
|||
|
|
|
|
|
|
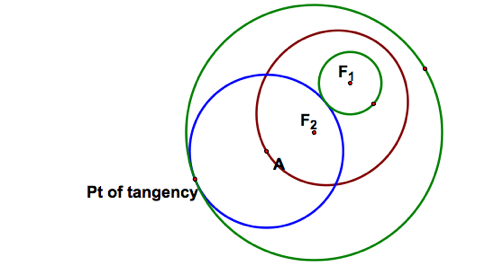
What is the locus of the center of the tangent circle? |
|
||
|
|
|
|
|
|
|
Hey the locus looks like an ellipse… Are we sure? If it is an ellipse, then the sum of the distances from any point to the two foci is constant. Click here to explore tutorial in GSP.
And in fact the sum of the distances is constant. |
||
|
|
|||
|
So, is the locus of the center of the tangent circle always an ellipse? |
|||
|
|
|||
|
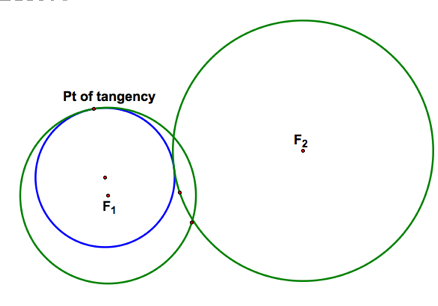
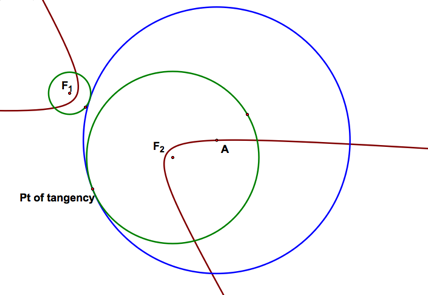
Case #3: The original circles are disjoint. |
|||
|
|
|||
|
|
|
|
|
|
What is the locus of the center of the tangent circle? |
|
||
|
|
Hey the locus looks like a hyperbola… Are we sure? If it is a hyperbola, then the difference of the distances from any point to the two foci is constant. Click here to explore tutorial in GSP.
And in fact the difference of the distances is constant. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|