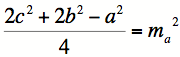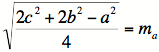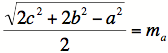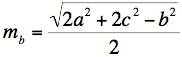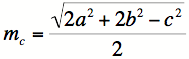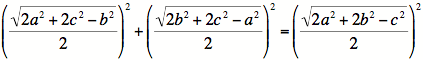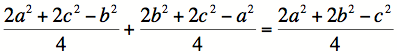Department of Mathematics and Science Education

J. Wilson, EMAT 6680

 

Allyson Hallman

 

 

Characterization of Medial Triangles formed from Equilateral and Isosceles Triangles

&

Characterization of Triangles whose Medians form Right Triangles

 

Part 1: Equilateral  Triangles

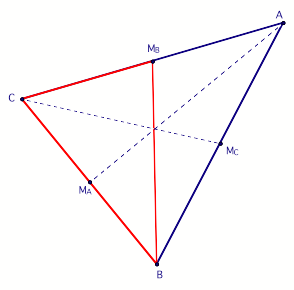
Consider an equilateral triangle and construct its medians. It should be easy to see that all three medians are congruent.

 

Not convinced?

 

Click here to explore the relationship between the three medians of an equilateral triangle in GSP.

 

Why might this be so?

 

In an equilateral triangle the medians of the triangle are also the altitudes. Can we prove it?

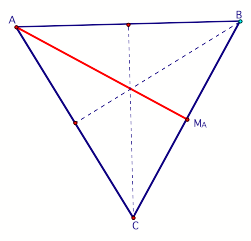
Take any median, in this case weÕve chosen ma (whose endpoints are A and Ma).

 

 because the sides of an equilateral triangle are congruent.

 

 by the reflexive property of congruence.

 

  because the midpoint of a segment divides that segment into two congruent segments.

 

Thus,  by the Side-Side-Side triangle congruence postulate.

 

 because corresponding parts of congruent triangles are congruent.

 

From the angle addition postulate, we know that , which in turn tells us that and   are supplementary angles.

 

If two angles are supplementary and congruent, then they must be right angles.

 

Because segments AMA and BC form right angles at MA, we can conclude that they are perpendicular at MA.

 

And so segment AMA is the perpendicular drawn from a vertex to the line containing the opposite side of the triangle, which in fact means that AMA  is an altitude with respect to side a of our triangle.

 

By similar argument we are able to show that each median is altitude of the triangle.

 

We know that the area of our triangle is constant no matter which altitude we use to calculate. LetÕs call our area R. Calculating the area using each of the three altitudes we have:

 

 

BMB  is an altitude with respect to side b of our triangle.

CMC  is an altitude with respect to side c of our triangle.

AMA  is an altitude with respect to side a of our triangle.

We know that all sides of an equilateral triangle are congruent and so we can call each side a. Substituting into two of our three formulas we have:

And then solving each for the median we generate the three following formulas:

And now, it should be quite obvious that having generated the same formula for each median that the medians of an equilateral triangle are in fact congruent and therefore the triangle formed by these congruent medians is equilateral. 

And so, we are now definitively convinced that the triangle formed by the medians of an equilateral triangle is itself equilateral. 

Does the same hold true for an isosceles triangles? Well, I am glad you asked.

 

 

 

Part 2: Isosceles Triangles

 

 

Consider an isosceles triangle and construct its medians.

 

We are hoping that two of our medians will be congruent and thus the medians of an isosceles triangle will form an isosceles triangle.

 

Need to explore medians of an isosceles triangle in GSP? Click here.

 

Hopefully, after some investigation in GSP, we suspect that the two medians drawn to the two congruent sides of the isosceles triangle are in fact congruent. How might we show this?

We are wanting to show that the green median and the red median are congruent. Could it be that the green triangle and the red triangle are congruent?

 

 by the reflexive property of congruence.

 

 because these are the congruent sides of the isosceles triangle.

 

 and because MC and MA are the midpoints of the AB and AC, respectively, and midpoints divide segments into two congruent segments.

 

Substitution gives us 

and then .

 

 because the angles opposite the congruent sides of a triangle are themselves congruent.

 

 by the Side-Angle-Side triangle congruence postulate.

 

And finally corresponding parts of congruent triangles are congruent and so  .

 

Thus we have shown that 2 medians of an isosceles triangle are congruent and so the medians of an isosceles triangle do in fact form an isosceles triangle.

 

 

 

Part 3: Right Triangles

 

 

Now, based on our two previous examples, surely the medians of a right triangle form a right triangle. Check it out. Click here for fun guided exploration.

Ah ha. We should be able to see that this is not the case for right triangles.

Well, if a right triangleÕs medians do not always form a right triangle, then what kind of triangle will always generate medians that form a right triangle.

WouldnÕt it be great if we could determine a relationship between the lengths of a median and the sides of a triangle.

 

Derivation for the formula of length of a median of a triangle in terms of the lengths of the sides of a triangle:

(it is kind of yucko, but worth the effort, so hang it there.)

 

We know that we can use HeronÕs formula to calculate the area of our triangle in terms of its three sides.

 

LetÕs simplify this formula:  where  or half the perimeter of our triangle.

 

 

Substituting in .

 

 

 

Distributing the  to three of the  terms

 

 

 

Combining like terms in each factor.

 

 

 

Factoring out  from each factor.

 

 

 

Simplifying the constant terms in radicand.

 

Looks like a lot of painful multiplication. However, if you remember difference of two squares, and do a little re-regrouping thanks to the associative property of addition we have:

 

 

 

Use associative property of addition to re-group terms in first two factors.

 

 

 

Factor out negative in 3rd term.

 

 

 

 

Recognize that the product of the first two factors under the radicand is the difference of two squares, as the product of the last two factors.

 

 

 

Just apply knowledge of squaring a binomial.

 

 

 

Distribute the negative in the 2nd factor.

 

 

 

Yucko multiplication. ThatÕs right kids multiplying two polynomials each with four terms. If you got this one right, thank your Algebra teacher.

 

 

 

Cancel out  terms and cancel out  terms.

 

 

 

Cancel out  terms.

 

 

 

Combine like terms. See it gets better.

 

 

 

 

A little factoring so everything looks good.

And so we have a simplified form of the heronÕs area of a triangle. LetÕs hang on to this one; it will come handy shortly.

 

 

 

 

 

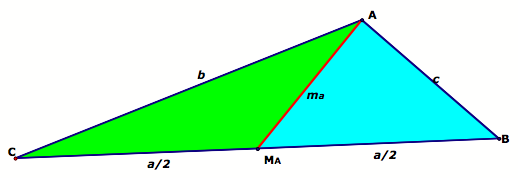
Now let us consider our triangle, with just one median drawn.

 

 

It is quite clear that the sum of the area of the two triangles formed by the median is equal to the sum of the original triangle. What is the relationship between the two triangles formed?

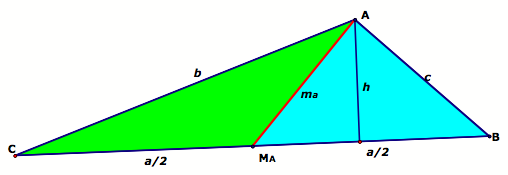
Consider the altitude drawn to side a of the original triangle. This is also the altitude of the green and blue triangles. It is the perpendicular segment from a vertex (A) of each of the three triangles drawn to the line containing the opposite side, (a). This height is also the height of the two other triangles.

Now we shall compute the area of our two triangles.

 

 

 

 

 

Hey, turns out that while the median doesnÕt divide the triangle into two congruent triangles, it does the divide the original triangle into two triangles whose areas are the same.

 

 

 

Now, using our simplified version of HeronÕs formula for the area of the triangle we will compute the area of the green and blue triangles, set them equal, and, with luck and our wonderful algebra skills, derive a formula for the length of a median in terms of the lengths of the sides of the original triangle.

 

 

 

Our simplified form of HeronÕs formula.

 

 

 

Substituting in the lengths of the three side of our green triangle.

 

 

 

Substituting in the lengths of the three side of our green triangle.

 

 

 

We showed earlier the areas are equal, and so substituting our area formulas in we have this equation.

 

 

 

Multiply both sides by 4 and squaring both sides.

 

 

 

Some distributing.

 

 

 

Adding  and  to both sides and subtracting  from both sides.

 

 

Collecting all terms containing .

 

 

Factoring out  on the right.

 

 

Factoring out  on the left.

 

 

Simplifying  and re-organizing. Do I notice a difference of two squares?

 

 

Yes, I do.

 

 

Factoring out  on the left.

 

 

Dividing both sides by , which is clearly not equal to 0. (Otherwise two of our triangle sides would be 0, and then we wouldnÕt have a triangle at all.)

 

 

Multiplying both sides by 2 to eliminate fractions.

 

 

Dividing both sides by 4.

 

 

Taking the square root of each side.

 

 

Simplifying our denominator. And at last we have it.

 

 

The length of a median is equal to half the square root of the difference of twice the sum of the squares of the two sides of the triangle that include the vertex the median is drawn from and the square of the side of the triangle the median is drawn to.

 

So our formulas for the remaining two medians are:

 

 

 

 

 

So what?

 

 

We are trying to determine what type of triangle will generate a triangle whose medians form a right triangle. What is always true of any right triangle?

Why that the sum of the squares of its legs equal the hypotenuse squared, of course.

So we should be able to dump the expressions for the lengths of the medians that we just generated, into our dear old friend, , and play around until we find some interesting relationship between the sides of the original triangle.

 

However, we need to be careful about this. If we start working away, with no regard for what a, b, and c represent in the original triangle we will ultimately find that c is smaller than a and b (how do I know? Because I did it already, so you need to trust me on this one), which poses a huge problem, as c should represent the longest side, not the shortest. 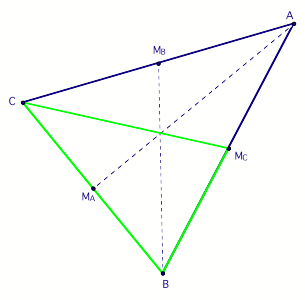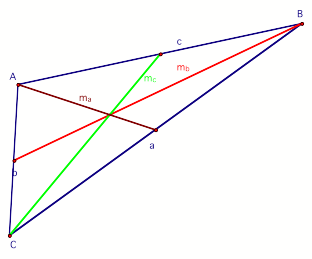So letÕs think about what our variables really represent in terms of our triangles, so that we can make some sense out of the conclusion we reach.

 

Consider any triangle and its three medians:

 

In the triangle pictured: we have labeled the longest side a, smallest side c, and remaining side b. Correspondingly, the shortest median, ma is the one drawn to the longest side, a, and the longest median, mc, is the one drawn to the shortest side, c.  So if the sides of the original triangle have the relationship: , then the medians will have the relationship: . This may not seem important now, but, hopefully when we reach our conclusion youÕll understanding the necessity of this step. Rest assured, IÕll explain it all again.

 

Now, we want the triangle formed by these three medians to be a right triangle. This means that the Pythagorean theorem must hold true for our triangle of medians. You might be inclined to just jump in with , however, these letters represent specific sides of our triangle. c is the hypotenuse, or longest side, so we must be sure that we are substituting the longest side in for c. Conveniently, in our triangle of medians we just determined the longest side to be mc . If the triangle of the medians is a right triangle, the following will hold true.

 

 

 

 

 

 

 

Substituting in our expressions for the medians of a triangle.

 

 

 

Squaring each term.

 

 

 

Multiplying both sides by 4.

 

 

 

Combining like terms on the left-hand side.

 

 

 

Adding c2 to both sides.

 

 

 

Subtracting a2 and b2 from both sides.

Here is where confusion could set in. Remember the important thing I mentioned in the beginning that you probably didnÕt really understand. Here it is. If you arenÕt thinking here, you could easily jump to the conclusion that fives times the square of the longest side of the original triangle is equal of the sum of the squares of its other two (shorter) sides, which now I hope makes no sense. Remember what a, b, and c really represent. a is the longest side of the original triangle, and c is the shortest side. So what we really have is:

 

 

 

 

 

If the triangle of the medians is a right triangle, then 5 times the square of the length of the shortest side of the original triangle will equal the sum of squares of the remaining sides of the original triangle.

 

 

 

 

 

One last thing, under what conditions are both the original triangle and the triangle of medians right triangles?

 

 

 

 

 

We know that for the triangle of the medians to be a right triangle,  must be true of the original triangle. For the original triangle to be a right triangle  must also be true. (Remember that a is the longest side of the original triangle.)

 

What values then must we have for the sides of the triangles for both of these equations to hold true?

 

 

 

 

Both  and  are true.

 

 

Substituting  into  we have:  and solving for b gives us:

 

 

 

 

 

 

 

 

 

Substituting this into  gives us , and then solving for a gives us:

 

 

 

 

 

Thus for both the original triangle and the triangle of the medians to be right triangles, the sides of the original triangle must be in the following ratio:

 

 

Summary of what weÕve proven:

1)     If the original triangle is equilateral, then the triangle of medians is also equilateral.

 

A]  The medians of an equilateral triangle are also the altitudes.

 

2)     If the original triangle is isosceles, then the triangle of the medians is also isosceles.

 

3)     If the triangle of the medians is right, then the 5 times the shortest side of the original triangle is equal to the sum of the square of the remaining two sides of the original triangle.

 

[A]   Simplified version of HeronÕs Formula for the area of triangle:

 

           [B]  A median of a triangle divides that triangle into two triangles whose areas are equal.

 

           [C] The length of a median of a triangle can be calculated from the lengths of the sides of the triangle using the following formula:

 

4)     If the original triangle is right, and the triangle of its medians is also right then, the ratio of the sides of the original triangle is .

 

Tired? Ready to leave? Return home.