HamiltonHardison’s Exploration of
Assignment 1: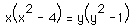 
From Jim
Wilson’s website: Examine:
.
See the graph.What happens if
the 4 is
replaced by other numbers (not necessarily integers)? Try 5, 3, 2, 1,
1.1, 0.9,
-3. Any unusual event?
Interpret.
What
equation would give the following graph:
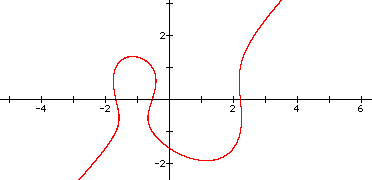
What
happens if a constant is added to one side of the equation? Try several
graphs
in some systematic way. Click here for one set of graphs.
Try
graphing
By exploring the graph of 
for various values of n, we
discover that there are three
classes of graphs: n<0,
0<
n < 1, n=1,
and n>1 .
For each of these classes, the y-intercepts will remain the same. The
y-intercepts occur when x = 0, so the
y-intercepts are solutions to 
. By factoring, we have 
. Every graph of the
form 
will have
will have
y-intercepts 0, 1, and -1.
When n > 1, we have a graph such
as
below. (Here with n = 4)
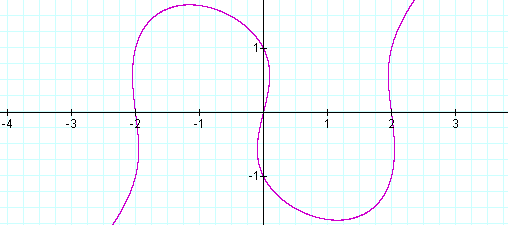
The most apparent characteristics of
this
graph are it’s intercepts.
Note that x-intercepts occur when y = 0, so
the x-intercepts are solutions to 
. By recognizing the
difference of two squares, we can solve this equation easily by
transforming it
to 
When
n > 1, we
have three x-intercepts:
.
When n = 1, we have:
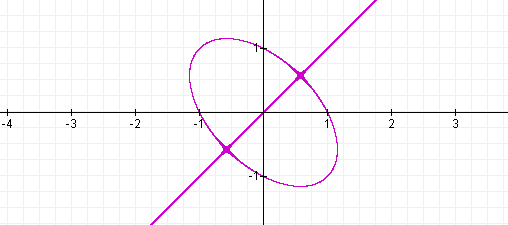
This graph appears to be the union of
an
ellipse and the line y=x. Algebraically,
we have: 
. So
. By distributing and
combining like terms, we have
. By
factoring, we arrive at 
. The zero product
property states that if the product of two numbers is zero, then one of
the two
numbers must be zero. So we have 
or 
. In the first case, means 
and we the line y = x
appears graphically as expected. In the
second case, we have 
,
which is an ellipse and confirms the second dominant shape
in the graphical representation.
When n < 1, we have a graph such
as
below. (Here with n = -4)
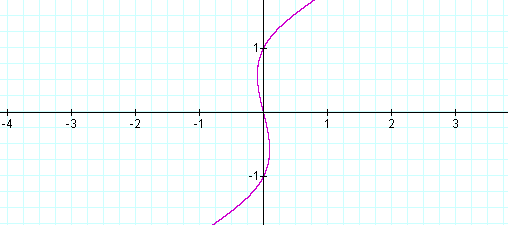
There is only one x-intercept in the
case
when n < 1. In factored form we have 
. For integers less
than 1, this means n is negative, or n
is zero. If n
is zero, the only solution to 
is x = 0. If n
is negative, one solution remains zero, while the remaining two
solutions are
complex.
When n
is between zero and 1, a case similar to when n > 1
occurs. This is the
result of three real solutions to the equation 
. The graph below
shows when n = .5
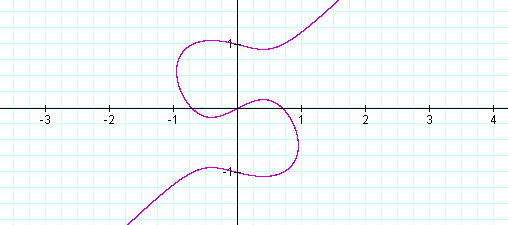
Returnto Hamilton Hardison's Page