
HamiltonHardison’s Exploration of
Assignment 12: Exponent Spreadsheet Exploration
Thanks
to Katie H., Madelyn K., and Kenny M. for being creative and asking the
questions
that created this exploration.
While
exploring properties of positive integer exponents in an algebra II
class, a
clever group of students noticed that if you took a number, lets say
99, and
raised it to the second power, you got a large number, (in this case
9801). By squaring the answer, a larger
number resulted (96059601). By repeating
the process over and over, the numbers got bigger and bigger until the
calculator returned an “overflow” error.
One
student asked: What would happen if you
raised
it to a smaller power, like 1?
The
students quickly discovered that repeatedly raising a number to the
first power
is not very interesting.
Another student asked: What would happen
if you raised it to a power like 1.5?
|
99 |
|
985.0375627 |
|
30915.70737 |
|
5435866.493 |
|
12673692703 |
The
students were quickly convinced that the same overflow error would
result.
An
interesting learning opportunity presented itself when a student asked,
“What
if you raised 10 to a number like .1?”
After
exploring 10 to the 1/10th power in the calculator, the students were
quickly
convinced that, after enough iterations,
the result of
the operations was one.


Very
impressed with the students thinking, I suggested:
What if we try a number like 99 and raise it
repeatedly to the .99 power?
The
TI-84 was not able to convince the students of a numerical result over
the
course of more than 10 minutes of key punching (and after having
swapped the calculator
between 3 different students).



As
they punched and punched away on the calculator, I made a simple excel spreadsheet. The first 200 iterations are shown below.
|
99 |
42.87892 |
21.62836 |
12.35734 |
7.817953 |
5.376096 |
3.957802 |
3.080788 |
2.510036 |
2.12276 |
|
94.55377 |
41.29728 |
20.97362 |
12.05052 |
7.658825 |
5.286428 |
3.903728 |
3.046318 |
2.487042 |
2.106842 |
|
90.34873 |
39.78893 |
20.34495 |
11.75427 |
7.504479 |
5.199131 |
3.850922 |
3.012572 |
2.464485 |
2.0912 |
|
86.36998 |
38.34993 |
19.74113 |
11.46816 |
7.35474 |
5.114126 |
3.799348 |
2.979532 |
2.442356 |
2.075829 |
|
82.60364 |
36.9766 |
19.16101 |
11.19177 |
7.209442 |
5.03134 |
3.74897 |
2.947179 |
2.420644 |
2.060724 |
|
79.03678 |
35.66545 |
18.60348 |
10.92471 |
7.068425 |
4.950703 |
3.699754 |
2.915496 |
2.399339 |
2.045877 |
|
75.65731 |
34.41321 |
18.06751 |
10.66659 |
6.931535 |
4.872145 |
3.651667 |
2.884466 |
2.378432 |
2.031285 |
|
72.45401 |
33.21681 |
17.55211 |
10.41707 |
6.798625 |
4.795601 |
3.604676 |
2.854071 |
2.357913 |
2.01694 |
|
69.41635 |
32.07335 |
17.05634 |
10.17579 |
6.669556 |
4.721006 |
3.558751 |
2.824295 |
2.337774 |
2.002839 |
|
66.53454 |
30.98011 |
16.57933 |
9.942426 |
6.54419 |
4.648301 |
3.513861 |
2.795123 |
2.318006 |
1.988977 |
|
63.79942 |
29.93451 |
16.12024 |
9.71667 |
6.4224 |
4.577425 |
3.469978 |
2.76654 |
2.2986 |
1.975347 |
|
61.20241 |
28.93413 |
15.67825 |
9.498221 |
6.304061 |
4.508323 |
3.427074 |
2.738531 |
2.279548 |
1.961945 |
|
58.73552 |
27.97669 |
15.25263 |
9.286795 |
6.189053 |
4.44094 |
3.385121 |
2.711081 |
2.260842 |
1.948768 |
|
56.39127 |
27.06003 |
14.84264 |
9.082119 |
6.077262 |
4.375223 |
3.344094 |
2.684176 |
2.242474 |
1.935809 |
|
54.16263 |
26.18213 |
14.44761 |
8.883934 |
5.968578 |
4.311121 |
3.303967 |
2.657804 |
2.224438 |
1.923064 |
|
52.04305 |
25.34107 |
14.06689 |
8.691991 |
5.862896 |
4.248585 |
3.264716 |
2.63195 |
2.206724 |
1.91053 |
|
50.02638 |
24.53504 |
13.69986 |
8.506053 |
5.760113 |
4.187568 |
3.226316 |
2.606603 |
2.189327 |
1.898202 |
|
48.10687 |
23.76232 |
13.34594 |
8.325892 |
5.660134 |
4.128024 |
3.188745 |
2.58175 |
2.172238 |
1.886075 |
|
46.27911 |
23.02131 |
13.00456 |
8.151293 |
5.562864 |
4.06991 |
3.151981 |
2.557378 |
2.155452 |
1.874146 |
|
44.53805 |
22.31047 |
12.67519 |
7.982046 |
5.468214 |
4.013183 |
3.116002 |
2.533478 |
2.138962 |
1.86241 |
By
cell 1000, excel gives 1.000200401, which is close to 1… But how could
they be
certain that the number didn’t go below one?
We
used Excel to plot a graph…
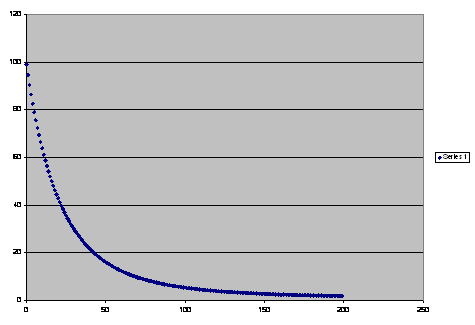
One
student said: Is that one of those “asym…things?”
While
we had not yet introduced the idea of rational exponents, exponential
functions, and had barely mentioned the word asymptote, the students
were able
to discover a lot of mathematics by using technology to develop
mathematical
thinking and questions.
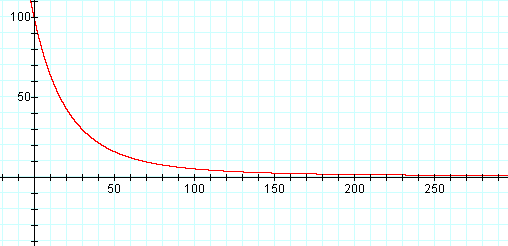
Algebraically,
we have the function 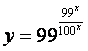 (,which
is shown above at right from graphing calculator).
(,which
is shown above at right from graphing calculator).
I
thought I was going off on a tangent during class (as I didn’t know
where the
exploration was going); it turns out it was just a secant, as I caught
back up
to the lesson of the day after a slight detour:
rational exponents.
Returnto Hamilton Hardison's Page