
HamiltonHardison’s Exploration of
Assignment 4: Proof of Concurrency of Medians
From
Jim
Wilson’s website: 14. Prove that the three medians of a triangle are
concurrent and that the point of concurrence, the centroid,
is two-thirds the distance from each vertex to the opposite side.
How
would you use GSP to help students understand this relationship of the triangle
and its medians? How would you develop a sense of proof of the relationship
with students?
We will attempt to prove that the medians of a
triangle, ABC, are concurrent by using coordinate geometry. We will set our origin at A, and side AB of
the triangle will lie on the x-Axis.
A has coordinates (0,0). B has coordinates (b, 0). C has coordinates (m ,
n).
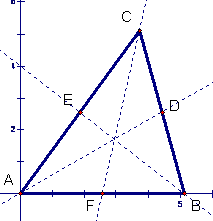
D is the midpoint of CB and has coordinates: ![]() The Median AD has
slope:
The Median AD has
slope: 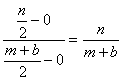
The Median AD lies on the line: ![]() .
.
E is the midpoint of AC and has coordinates: ![]() The median BE has
slope:
The median BE has
slope: 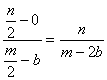
The median BE lies on the line: ![]()
F is the midpoint of AB and has coordinates: ![]() The median CF has slope:
The median CF has slope:
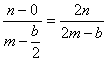
The median CF lies on the line: ![]() .
.
We will now find the intersection of the lines
containing medians AD and BE.![]() and
and
![]() give
give ![]() . Solving for x yields
. Solving for x yields ![]() . So centroid1
has coordinates:
. So centroid1
has coordinates: ![]() .
.
The intersection of the lines containing medians AD
and CF can be found by using ![]() and
and ![]() .
.
Solving ![]() for x yields
for x yields ![]() . So centroid2
has coordinates:
. So centroid2
has coordinates: ![]()
The intersection of lines containing medians BE and CF
can be found by solving ![]() .
.
Solving for x
gives ![]() . So centroid3
has coordinates:
. So centroid3
has coordinates: ![]() .
.
Since the three lines containing the medians have the
same point of intersection, the lines containing the medians are concurrent.
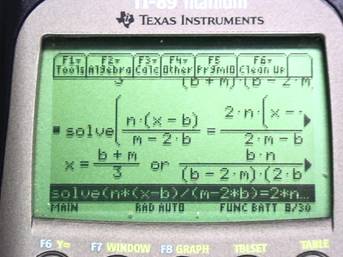
(Note: Much of
the symbol pushing for solving the equations was done by using the Computer
Algebra System (CAS) on the TI-89. A
classroom demonstration using a CAS might be a quick and convincing way to
prove the concurrency of medians to high school students without getting bogged
down in symbol manipulation.)
Show that the centroid lies 2/3 of the distance from the vertex to the midpoint of
the opposite side:
Let’s consider the median AD. D has coordinates ![]() . The centroid has coordinates
. The centroid has coordinates ![]() . By similar
triangles, we
. By similar
triangles, we
can take
the ratio of the abscissas and the ratio of the ordinates and see that both are
equal to 2/3 as desired.
Returnto Hamilton Hardison's Page