HamiltonHardison’s Exploration of
Assignment 8: An Altitude and Area Proof
From
Jim
Wilson’s
website: Construct any acute triangle ABC and its circumcircle.
Construct the three altitudes AD, BE, and CF. Extend each altitude to
its
intersection with the circumcircle at
corresponding
points P, Q, and R.
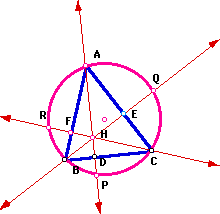
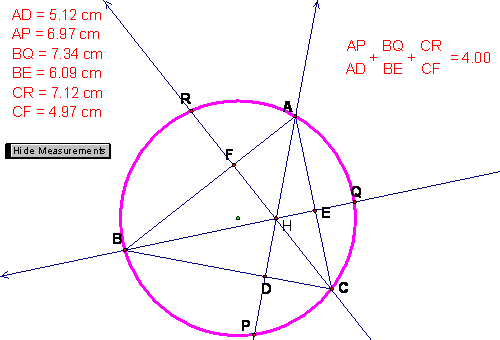
Find
.
Click
HERE
for a GSP sketch.
Upon
investigation it appears that 
.
It
may be helpful to add some line segments.
In order to find similar and congruent
triangles.
Here we can
see that 
by angle-angle similarity
(Red and Blue) (Apologies if colors
do not show up on some computers). Since
BE is an altitude,
HEC is a right angle. Since CF is an
altitude, HFB is a right angle. Angles EHC
and FHB are vertical angles. We also
have 
by angle-angle
similarity (Red and Yellow). Since
Since and ,
. Since FB is
congruent to itself, we have that the blue and yellow triangles are
congruent, or 
. A similar argument shows
that 
. Now we have the two
larger triangles, 
.
From
similar reasoning we have:
; 
; 
The
area of quadrilateral 
. The area of quadrilateral
. The area of quadrilateral 
By
triangle congruence, the sum of the blue areas (triangles BPC, CQA, and
ARB) is equal to the area of
the
triangle ABC. By adding the area of each
of
the quadrilaterals described above, we are computing 4-times the area
of
triangle ABC, (3 yellow triangles ABC and 3 blue triangles equal in
area to ABC).
. For convenience, we
will write:
.
We
can compute the area of ABC by using the altitudes as well. 
.
Now
we can combine our equations cleverly.
. Since AB is
congruent to itself, we have 
as desired.
Returnto Hamilton Hardison's Page