
Hamilton
Assignment 9: Pedal Triangles
From
Jim Wilson’s assignment
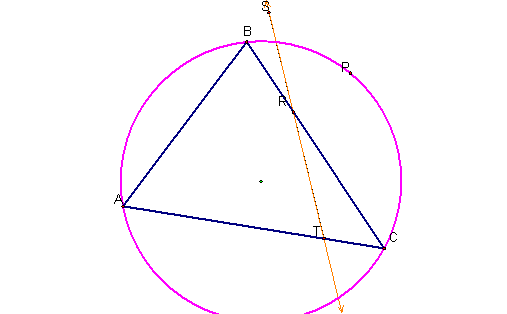
page: 1a. Let triangle ABC be any triangle. Then if
P is any point in the plane, then the triangle formed by constructing
perpendiculars to the sides of ABC (extended if necessary) locate three points
R, S, and T that are the intersections. Triangle RST is the Pedal
Triangle for
9. Find all conditions in
which the three vertices of the Pedal triangle are colinear
(that is, it is a degenerate triangle). This line is called the Simson Line.
By exploration, it can be discovered that the pedal
triangle becomes degenerate when P lies on a vertex of the triangle. The placing P on the circumcircle
might be a good bet for finding all such places. (This can be easily done using the merge
point feature in the edit menu).
Locate the midpoints of the sides of the Pedal
Triangle. Construct a circle with center at the circumcenter
of triangle ABC such that the radius is larger than the radius of the circumcircle. Trace the locus of the midpoints of the sides
of the Pedal Triangle as the Pedal Point P is animated around the circle you
have constructed. What are the three paths?

The three paths appear to be
ellipses. Very
interesting construction and fun to animate.
Repeat where the path is the circumcircle.
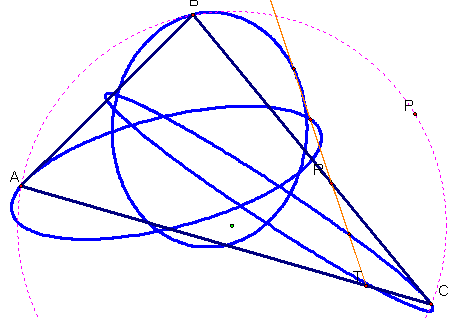
In this case the paths traced by the midpoints still appear to be ellipses, but
these each ellipse passes through one vertex of the original triangle.
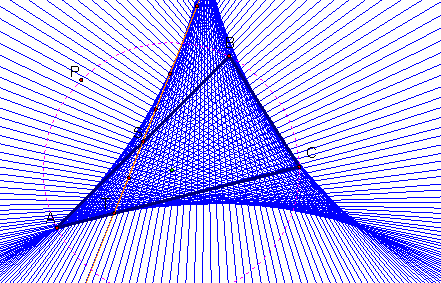
In particular, find the
envelope of the Simson line as the Pedal point is
moved along the circumcircle.
Returnto Hamilton Hardison's Page
