HamiltonHardison’s Exploration of

Final Assignment: Bouncy Barney

A. Bouncing Barney. We discussed this investigation in class. Your challenge now is to prepare a write-up on it, exploring the underlying mathematics ideas and conjectures.

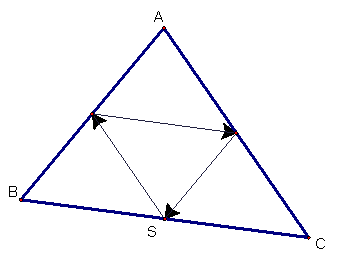
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

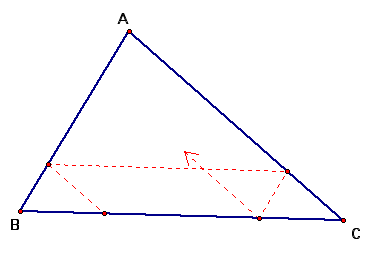
I assume some GSP sketches and explorations will be useful. A highly regarded write-up will examine the extensions and interpretations of this exploration.

It appears, based on investigation in GSP, that Barney will return to his starting point S.

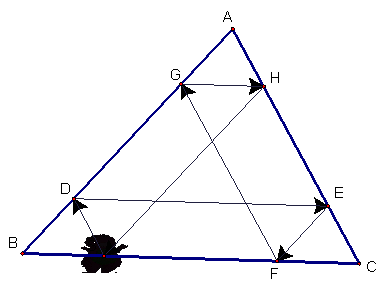
Proof that Barney will finish where he started:

Barney starts at some point S on BC and moves parallel to AC until he hits the wall AB at point D. Since SD is parallel to AC and angle B is congruent to itself, we have angle-angle similarity between triangles DBS and ABC.

Barney then bounces from D to point E on AC, creating ADE similar to ABC.

From E to F on BC, with EFC similar to ABC.

From F to G on AB, with GBF similar to ABC.

From G to H on AC, with AGH similar to ABC.

From H to I on BC, with HIC similar to ABC.

The goal is to Prove that Barney’s starting point, S, is the same as his stopping point, I.

Since , we have . We know that by segment addition, so we have . So .

Since , we have . So . By segment addition, . So .

Since , we have . So .

Therefore, . By segment addition, we know that . By combining these final two equations, we arrive at , or .

So Barney’s starting point, S, and ending point, I, are the same distance from C and between B and C. So S and I are the same point.

(Whew… I know there is an easier way to do this!)

This means Barney hits each wall twice on his journey back to his starting point.

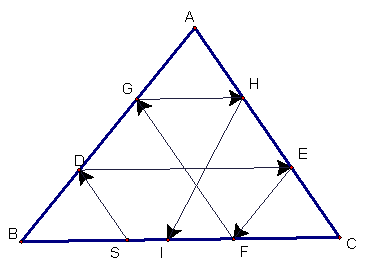
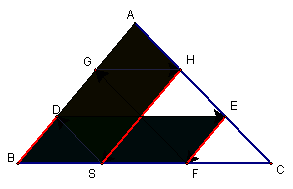
Now that we know Barney’s path looks something like what is pictured below:

We can investigate a few interesting aspects of the problem. If Barney’s starting point, S, is the Midpoint of BC. We know from similar triangles (and the monstrous manipulations above) that . Since S is the midpoint, , so . This means that BF=BS. In this case, points F and

S are the same and Barney will be back at the beginning in half the usual number of bounces. In this case, Barney has traced the medial triangle in his journey across the room.

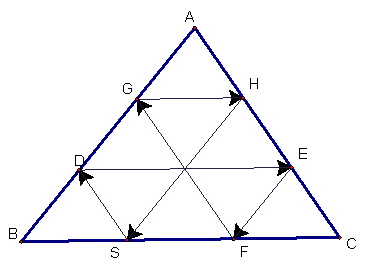
Now that we know a bit about Barney’s path, we can see that Barney traces out parallelograms as well as triangles.

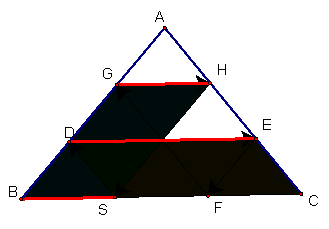
The yellow quadrilateral DECS is a parallelogram since DE is parallel to SC and SD is parallel to EC (similar arguments hold for the other parallelograms). Since opposite sides in parallelograms are congruent, we have DE = SC from the yellow parallelogram. The blue quadrilateral is also a parallelogram, so we have GH = BS.

Barney’s path length is given by: SD + DE + EF + FG + GH + HS. From various Parallelograms, we see that SD = EC, DE = BF, EF = BD, FG = AE, GH = BS, and HS = AD. So Barney’s path length is EC + SC + BD + AE + BS + AD. By regrouping, we see (BS + SC) + (EC + AE) + (AD +BD) = BC + AC + AB. This means Barney’s path is equal in length to the perimeter of the triangle.

Send me an e-mail

Returnto Hamilton Hardison's Page

Return to EMAT6680 Page