HamiltonHardison’s Exploration of
Cevva’s Theorem
From Jim
Wilson’s website:
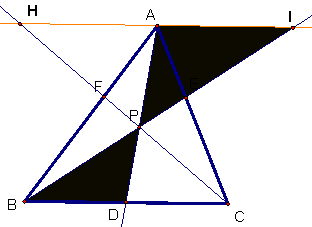
Ceva's Theorem. Consider any triangle ABC. Select a point P inside the
triangle and draw lines AP, BP, and CP extended to their intersections with the
opposite sides in points D, E, and F respectively.
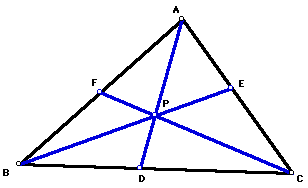
1. Explore (AF)(BD)(EC)
and (FB)(DC)(EA) for various triangles and various locations of P.
2. Conjecture? Prove it!
(you may need draw some parallel lines to produce some
similar triangles, OR, you made need to consider areas of triangles within the
figure) Also, it probably helps to consider the ratio
3. In your write-up, after the proof, you might want to discuss how this theorem could be used for proving concurrency of the medians (if P is the centroid), the lines of the altitudes (if P is the orthocenter), the bisectors of the angles (if P is the incenter), or the perpendicular bisectors of the sides (if P is the circumcenter). Concurrency of other special points?
4. Explore a generalization
of the result (using lines rather than segments to construct ABC) so that point
P can be outside the triangle. Show a working GSP sketch.
Investigation:
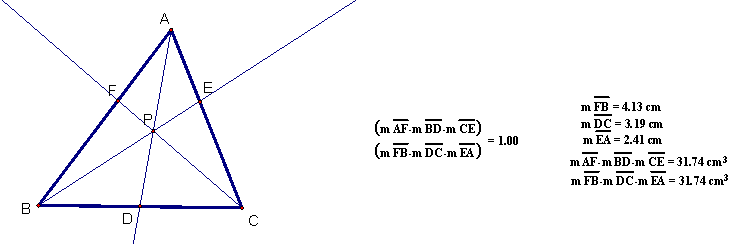
By constructing a GSP sketch
and exploring measurements, it appears that 
.
Proof:
At the advice of Clay Kitchings, I began by drawing a line parallel to BC through
A and began looking for similar triangles.
The following pairs of similar triangles appeared as a result of
Angle-Angle Similarity due to vertical and alternate-interior angles. For visualization purposes, the interiors of
the desired triangles have been shaded.
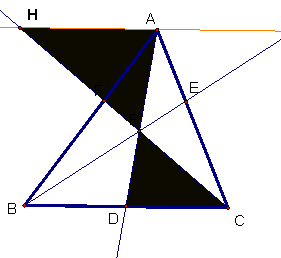
1. 
2. 
3. 
4. 
From the pairs of
similar triangles, we can now investigate several ratios:
From 1: 
From
2: 
From
3: 
From
4: 
By combining ratios 1
and 3 (since 
), we have 
. (ratio 5)
From ratio 2, we
have: 
(6). From ratio 4, we
have: 
(7).
By replacing AI and AH
in ratio 5 with the results from equations (6) and (7), we have
.
By multiplication, we
can transform this equation to 
.
Since 
, their ratio is 1. So
our result is 
. Or
, as
desired.
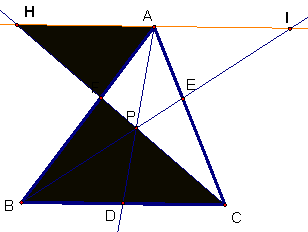
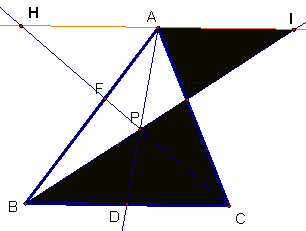
General Case:
Here
is a sketch to investigate cases when p
is outside of the triangle.
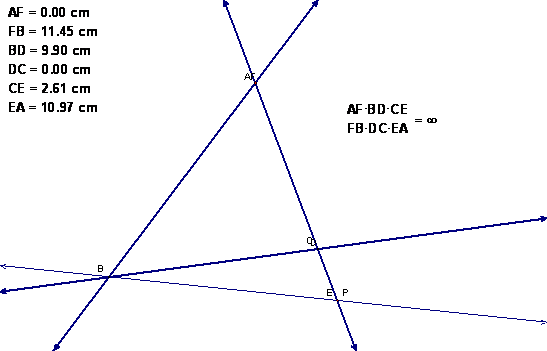
It appears that the
theorem holds as long as p does not
line on the lines AB, BC, or CB as this will result in an indeterminant
expression (which GSP has some difficulty handling as it reports zero,
undefined, infinity, or numerical values).
To investigate this case, select point p and one of the lines.
Then, from the edit menu, select merge point to line.
Returnto Hamilton Hardison's Page