µ µ
µ
Tiffany N. KeysŐ Essay 2:
NapoleonŐs
Triangle
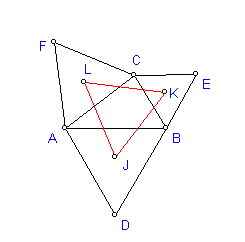
INVESTIGATION: Given any triangle ABC, construct
equilateral triangles on each side and find the center of each equilateral
triangle. The triangle formed by these three centers is Napoleon's Triangle.
Step
1: Given triangle
ABC, construct the point D such that ABD is an equilateral triangle, and D and
C are on opposite sides of AB.
Step
2: Construct the
point E such that BCE is equilateral.
Step
3: Construct the
point F such that CAF is equilateral.
Step
4: Let J be the
center of ABD, K the center of BCE, and L the center of CAF.
Step
5: Then JKL is
Napoleon's triangle.
PROOF
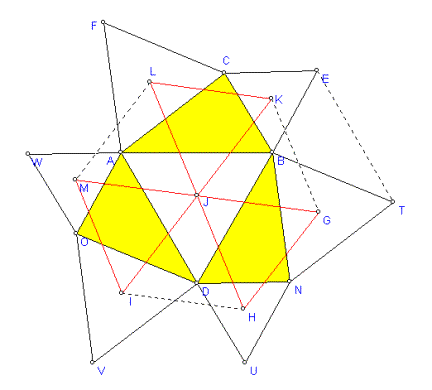
Step
1: Construct the
point O such that triangles DAO and ABC are congruent.
Step
2: Construct the
point N such that BDN and ABC are congruent.
Step
3: Construct the
Napoleon triangles JMI and JGH from triangles DAO and BDN.
Step
4: Considering
triangle TEB, it is assumed that BE = BC and BT = BN = AC.
Step
5: Since angle DBN
is equal to angle BAC, it is assumed that <EBT = 180 - <ABC - <BAC =
<ACB.
This shows that triangle TEB must be
congruent to triangle ABC by SAS.
Step
6; By
construction, GK = KL, which also shows that GK = KL = LM = MI = IH = HG.
Step
7: JL = JG by
construction, GK = LK by STEP 6, and JK = JK, so that triangles GJK and LJK are
congruent by SSS.
Step
8: Therefore we
can assume <KJG = <LJK and that the six angles at J must all be congruent
and all are 60ˇ.
Step
9: Since <LJK =
60 degrees, we can assume that <JKL and <KLJ are 60ˇ.
Step
10: In conclusion, triangle
JKL is equilateral.