Tiffany N. Keys’ Assignment 12:

Altitude of a Hot-Air Balloon

An Exploration using Microsoft Excel

Construct a graph of any function y = f(x) by generating a table of values with the x values in one column and the y values in another.

Elise is at an altitude of 250 feet in a See-The-World hot-air balloon. She turns on the burner and the balloon rises at a rate of 20 feet per minute for 20 minutes. Her altitude h after you have risen for t minutes is given by the function

h = 250 + 20t, where 0 < t < 20 (or y = 20x + 250)

Rodney is at an altitude of 250 feet in a Capture-The-View hot-air balloon. He turns on the burner and the balloon rises at a rate of 25 feet per minute for 20 minutes. His altitude h after you have risen for t minutes is given by the function

h = 250 + 25t, where 0 < t < 25 (or y = 25x + 250)

Let’s enter these functions into Excel to see how they would be represented graphically.

Time (minutes)	See-The-World Balloon	Capture-The-View
0	250	250
1	270	275
2	290	300
3	310	325
4	330	350
5	350	375
6	370	400
7	390	425
8	410	450
9	430	475
10	450	500
11	470	525
12	490	550
13	510	575
14	530	600
15	550	625
16	570	650
17	590	675
18	610	700
19	630	725
20	650	750

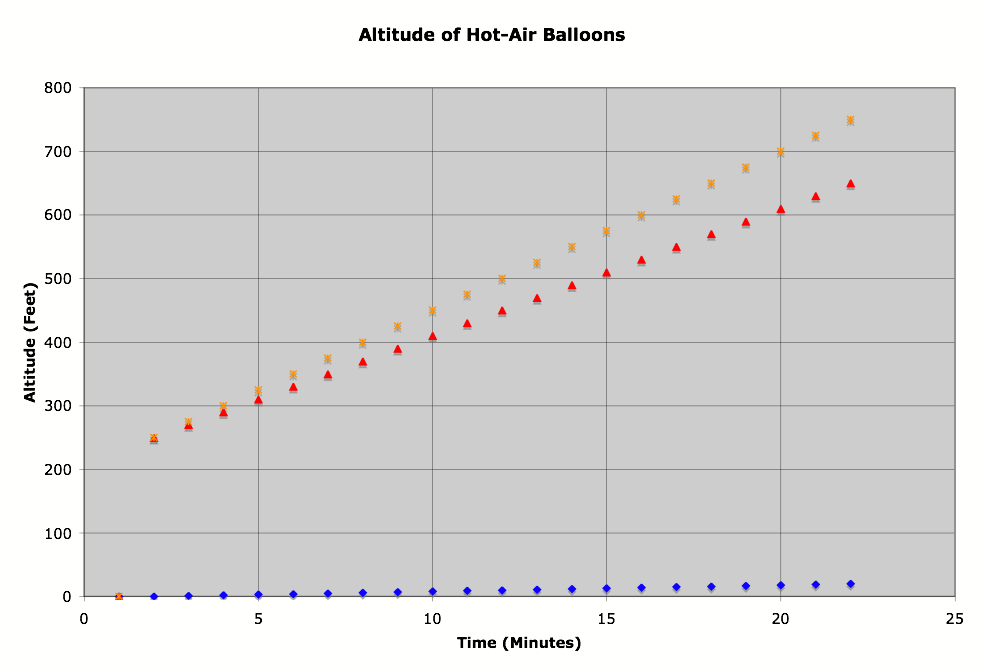
PORPOSED QUESTIONS:

· From the graph of the functions, can we conclude which balloon would reach 1000 feet the fastest?

· Can we use the graph of the functions to figure out how long it would take for each balloon to reach 1000 feet?

· What other conclusions can be made from the graph?

Return to Tiffany N. Keys’ Homepage