Tiffany N. KeysÕ Assignment 3:
Locus of
the Vertex
INVESTIGATION: Consider the locus of the vertices of the set of
parabolas graphed from y = x2 + bx + 1. Show that the locus is the
parabola y = -x2 +1.
Generalize.
In
order to generalize that the locus of vertices of the set of parabolas graphed
from y = ax2 + bx + c, you can explore the equation with different
values of a, b, or c as the other two are held constant.
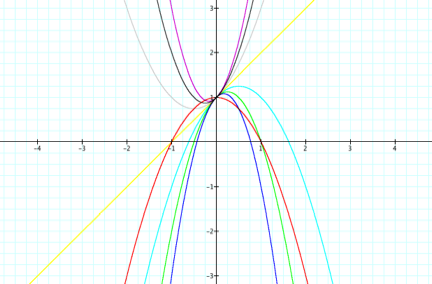
For
a = -3, -2, -1, 0, 1, 2, 3, the following
overlay graphs are obtained.
Observations:
á
Each
parabola always passes through (0, 1) on the y-axis.
á
The
vertex of each parabola changes as the value of a
is changed in the equation.
á
The
concavity of each parabola also changes when a different value of a is substituted in each equation.
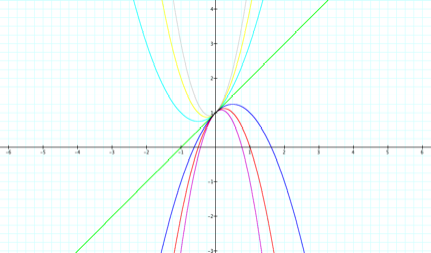
For
b = -3, -2, -1, 0, 1, 2, 3, the following
overlay of graphs are obtained:
Observations:
á
Like
the graphs above, each parabola passes through (0, 1) on the y-axis.
á
The
vertex of each parabola also appears to change in each equation as the different
values of b are substituted in.
á
The
concavity of each parabola appeared to remain the same.
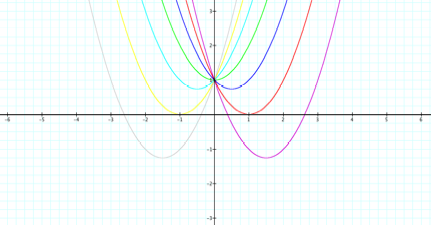
Lastly,
where c = -3, -2, -1, 0, 1, 2, 3, the
following overlay of graphs are obtained:
Observations:
á
Each
parabola does not pass through the same point as the value c is changed.
á
Again,
the vertex of the parabola changes in each equation.
á
The
concavity of the parabola increased as the value of c
was increased.
We
can generalize that because all of the graphs passed through the point (0, 1)
on the y-axis that y = -x2 + 1 is the locus
of vertices of y = ax2 + bx + c, despite the fact that when
the value of c was changed.