Tiffany N. KeysŐ Assignment 6:
The
Exploration of Parabolas Using GSP
A parabola is the set of points equidistant
from a line, called the directrix, and a fixed point, called the focus. Assume
the focus is not on the line. Construct a parabola given a fixed point for the
focus and a line (segment) for the directrix.
á
Use
an Action Button to generate the parabola from an animation and trace of a
constructed point.
á
Repeat
9a with a trace of the tangent line at the constructed point.
á
Use
the locus command to generated the parabola from a constructed point or the
tangent line at that point.
Steps
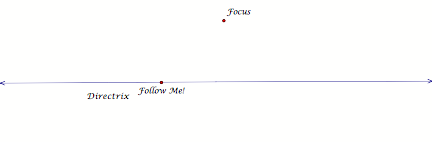
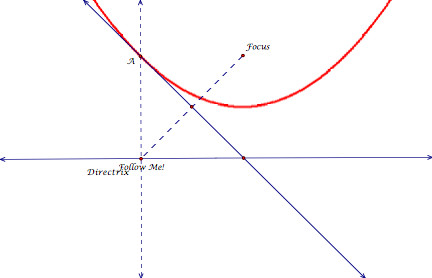
1: Construct a line (the directrix) and a point not on
the line (the focus).
Construct
a point on the line and label it "Follow Me".
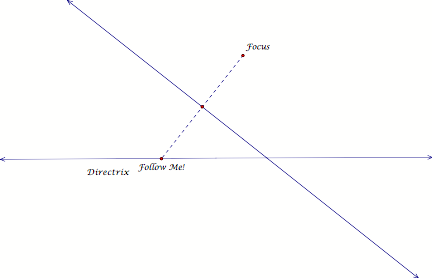
Step
2: Construct a segment from the
Focus to the Follow Me point.
Create
a perpendicular bisector of that segment.
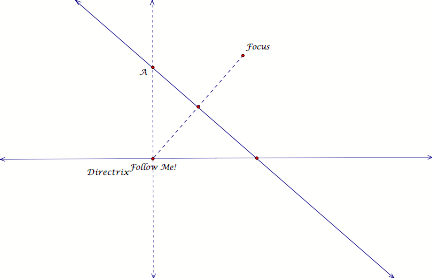
Step
3: Construct the perpendicular that
intersects the directrix at the Follow Me point.
Label
the intersection of this line and the line constructed in Step 2 as point A.
Step
4: Trace the intersection A and
animate the Floow Me point.
As
the Follow Me point moves along the directrix it will create a parabolic shape.
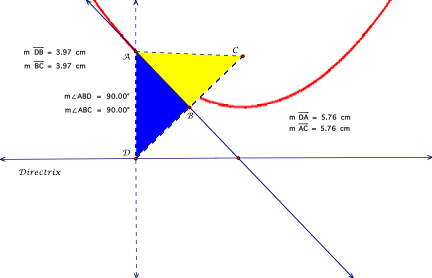
PROOF:
As
stated in Step 2, line AB is the perpendicular bisector of segment CD. Therefore, segment DB is congruent to
segment BC, and angle ABC is congruent to angle ABD. If the segment AC is constructed, two triangles are formed
sharing a segment AB. The
Side-Angle-Side Congruence Axiom states that if two sides and the included
angle of one triangle are congruent respectively to two sides and the included
angle of another triangle, then the two triangles are congruent. Segments AD and AC are congruent as a
result of this, therefore proving that this construction is in fact a parabola.