
Tiffany N. KeysŐ Assignment 8:
Altitudes
and Orthocenters
The
orthocenter of a triangle is the common intersection of the three lines
containing the altitudes. The orthocenter does not have to be on the segments
that are altitudes, but can lie on the line extended along the altitude.
An
altitude of a triangle is a perpendicular segment from any vertex to the line
of the opposite side.
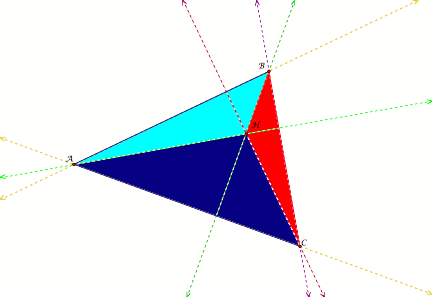
1. Construct any
triangle ABC.
2.
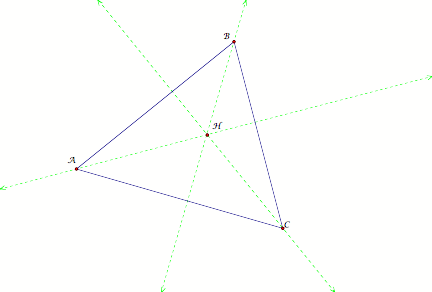
Construct the
Orthocenter H of triangle ABC.
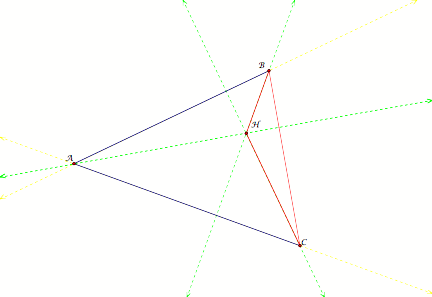
3. Construct the
Orthocenter A of triangle HBC.
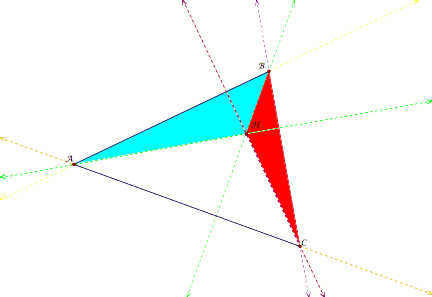
4. Construct the
Orthocenter C of triangle HAB.
5. Construct the
Orthocenter B of triangle HAC.
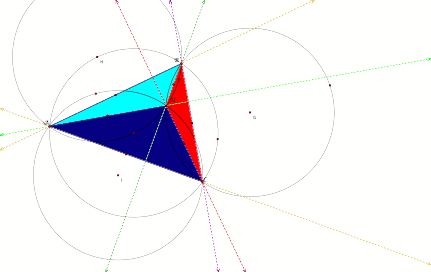
6. Construct the
Circumcircles of triangles ABC, HBC, HAB, and HAC.
OBSERVATIONS:
á
The
altitudes of triangle ABC divided the triangle into three separate triangles.
á
All
of the interior triangles are obtuse triangles.
á
The
orthocenter of an interior triangle of the larger angle is coincident with the
vertex of triangle ABC that is not on the interior triangle.
á
All
of the circumcircles appear to be congruent .