
Carisa
Lindsay
Assignment
11
Exploration
of Polar Equations
We
are going to explore what happens when we change various values in the
following equation:
![]()
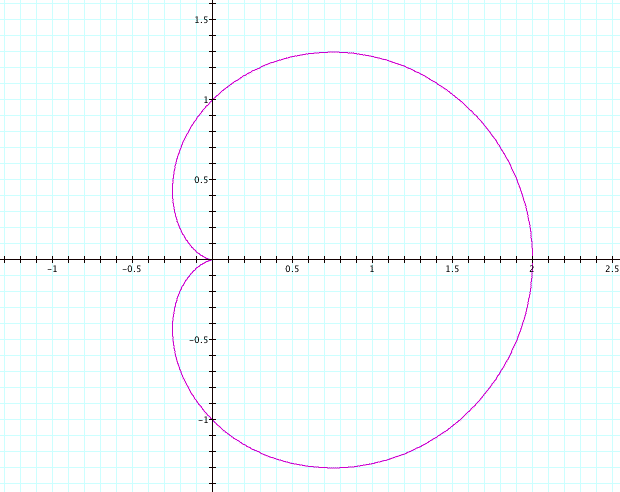
First,
we need to see what the most basic graph looks like.† Suppose a
= b = k = 1.
Letís
explore the values of a while b and k are constant.
As
the absolute value of a increases,
the radius of the circle grows.
However,
something interesting occurs for rational values of a between -1 and 1.† The graph is transitioning into various sized
pedals.
We
can conclude the value of a affects
the actual size and shape of the graph.
Now
we can explore what happens when we change the k value in the equation
†![]() .
.
We
will maintain b as a constant of 1
and allow 0£q£2p.
Suppose
k=1
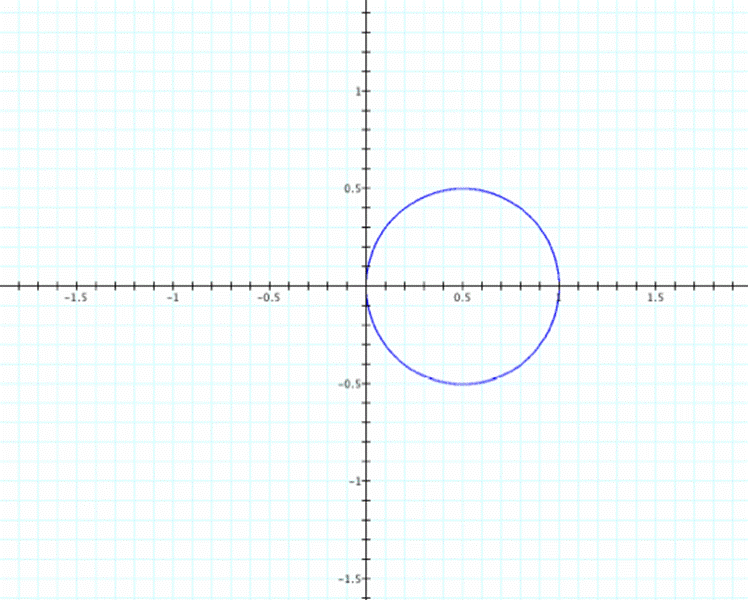
We
see a circle of radius 0.5 and centered at (0.5,0).†
What
if we try k=2?
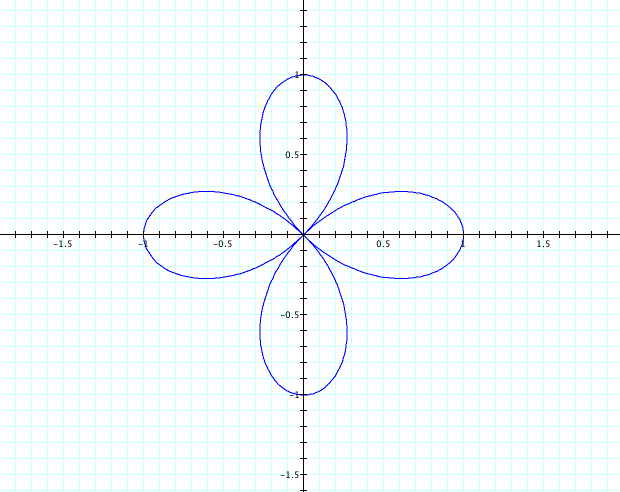
We
have a 4-pedaled flower centered at the origin with pedal unit length.
What
if we try k=4?
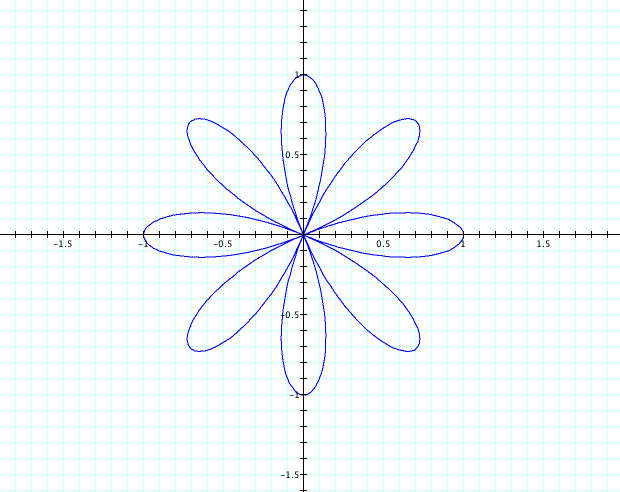
Now
we have an 8-pedaled flower centered at the origin with pedal unit length.
If
we try other even-numbered integers, we will see similar results- that is
2k-pedaled flower centered at the origin with pedals unit length.
For
instance, letís consider k=10.† We can
predict that we will see 20 pedals of unit length centered at the origin.
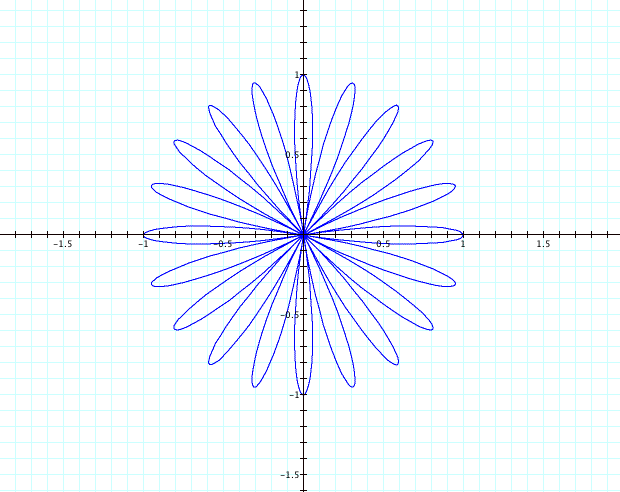
What
happens for odd-integer k-values?
Suppose
k=3.
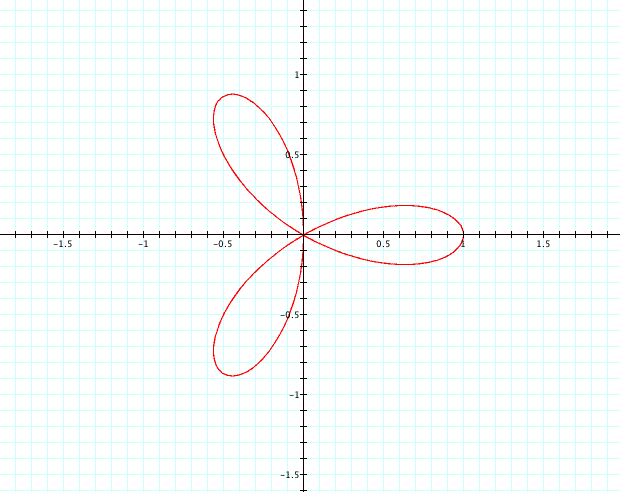
It
does not appear to follow the 2k pattern, but it maintains unit length pedals
and centered at the origin.
Letís
find out if the pattern holds true for k=5.†
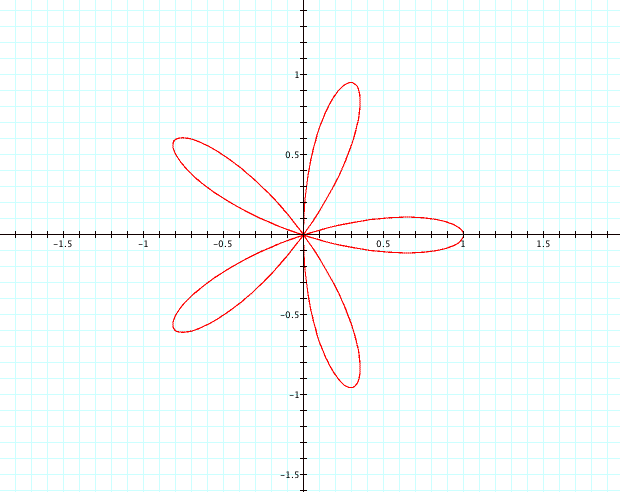
So
far our conclusions are correct.† Letís
try k=13.
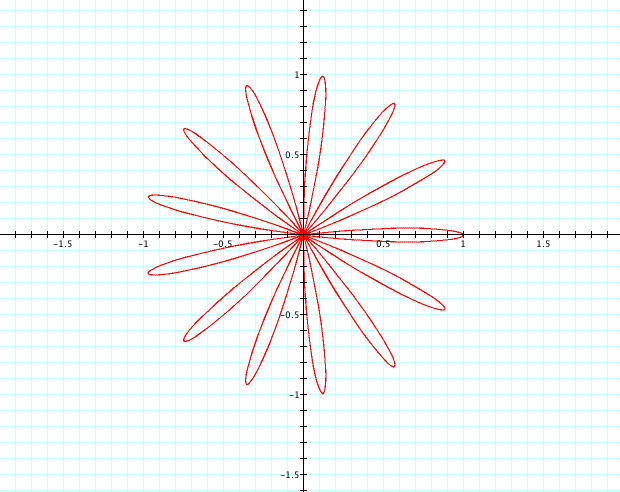
We
can conclude for even-numbered integer values of k, we will yield a result of
2k pedals, all unit length and centered at the origin.† However, for odd-numbered integer values of
k, we will see k pedals which are also unit length and centered at the
origin.†
What
if k is not an integer?†
Suppose
k is only ďpartĒ of a whole number, or a rational number.
For
values of k between 0 and 1, we see only part of the flower.† Instead we see various pedal shapes, but not
in entirety.
However,
if we set the values of k to be between 0 and 5 (that is, including rational
and irrational numbers), we can watch the graph transition between the
different k-pedaled flowers.
Letís
consider what would happen if we used the sine function rather than
cosine.† Let us use the following
equation for the remainder of the exploration:
![]()
Just
like with cosine, letís first look at b=k=1.†
For comparison, cosine is in the color blue while the sine equation is
in gray.
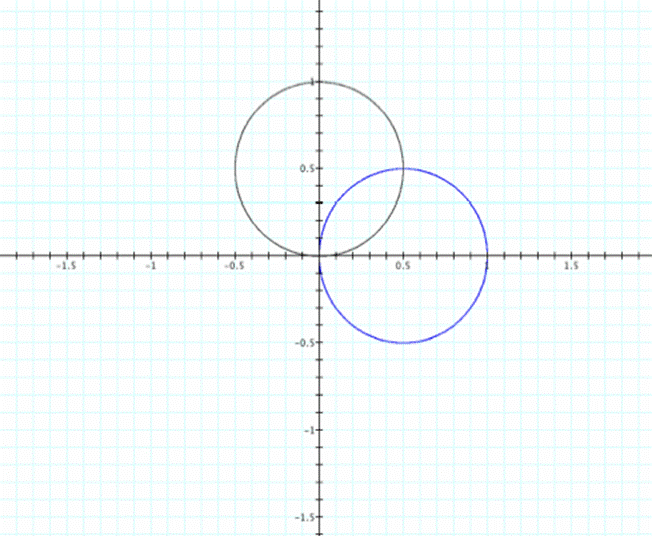
So
far, these graphs appear to be very similar except for where the center is
located.† For the sine graph, the center
is on the y-axis at (0,0.5).
Letís
try various values of k:
k=2
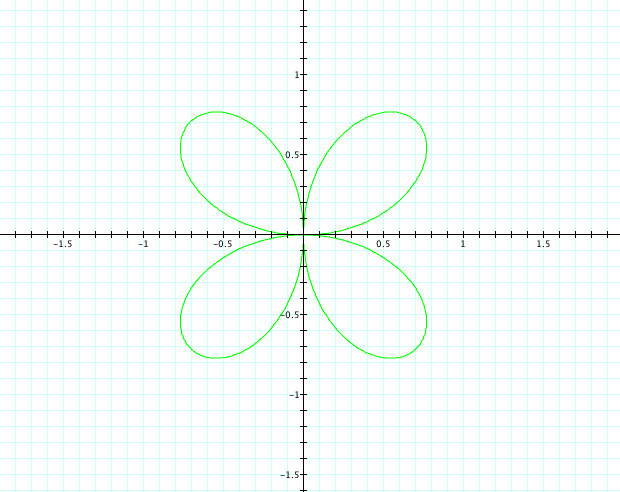
We
again see the trend of 2k pedals, but the flower is simply rotated 45
degrees.†
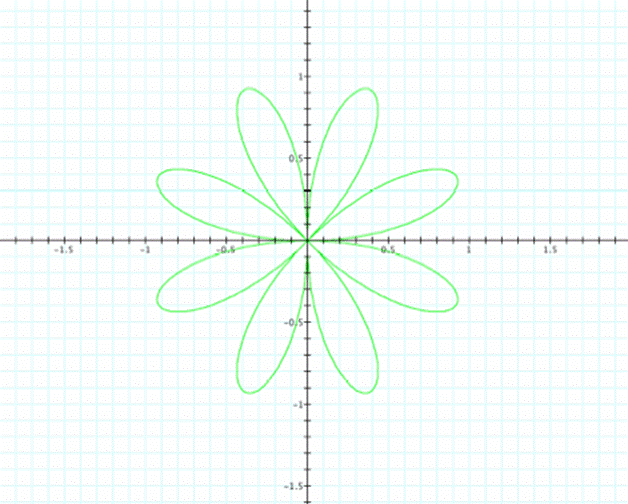
k=4
k=3

We
again see k-pedals with odd integer values of k.
Lastly,
letís verify what will happen with rational values of k.
Not
surprisingly, we see similar results as the cosine equation.†