
Carisa
Lindsay
Assignment
12
Analysis
of Tree Data
This
is a comparison of how much lumber a tree will produce given its age in
years. Given the following data:
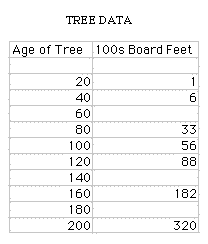
We can
make predictions based on the behavior of this data. Using an Excel spreadsheet, we can model this
data using some sort of exponential growth.
Exponential growth curves are “nice” for approximation primarily because
they are smooth and the end-behavior is very clear (it’s going up!). But, this graph isn’t truly exponential
because it is not quite as steep and the age of a tree vs. its age is hardly
exponential (as compared to situations such as population growth). So, we should consider other smooth curves
such as a polynomial. Even-powered
polynomials make the best choices because they also have an end behavior of
increasing to infinity. Odd-powered
polynomials are not as reliable since one side is always decreasing. We are most familiar with polynomials of
degree 2, so a quadratic equation would make an appropriate approximation.
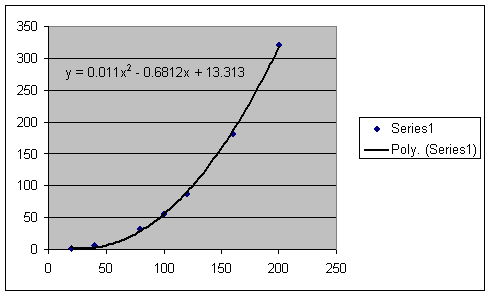
As you
can see, a quadratic regression line is very good. However, we can get a better line:
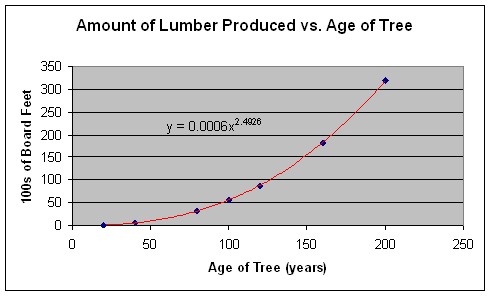
We
are missing some ages of tree data.
Using this function model, we can predict how much lumber a sixty-year
old tree will produce. In order to make
this calculation, I will simply substitute “60” in for x in the equation model.
![]()
![]()
So, a sixty-year old tree will
produce approximately 1600 board feet.
We can make similar
calculations for 140 year-old and 180 year-old trees:
![]()
![]()
![]()
![]()
Thus, a 140 year-old tree
will produce approximately 13,400 board feet and a 180 year-old tree will
produce approximately 25,000 board feet.
Based on this data, we can conclude the older the tree, the more board
feet it will produce.