
Carisa
Lindsay
Assignment
2
Exploration
of Parabolas
This
is an exploration of parabolas as we change the quadratic coefficient, the
linear coefficient, and the constant term. We will analyze how each of these terms affects the shape of
the parabola.
First,
we will keep the quadratic and linear terms a constant value of one and vary
the constant term from -5 to -1.
a
= 1, b = 1, c = -5... -1
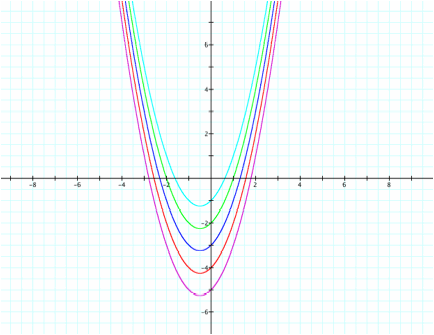
As
you can see, the vertex of the parabola translates vertically and approaches
the x-axis as c increases.
Again,
if we maintain the quadratic and linear terms as one, the parabola will
translate vertically as c increases.
a
= 1, b = 1, c = 0...5
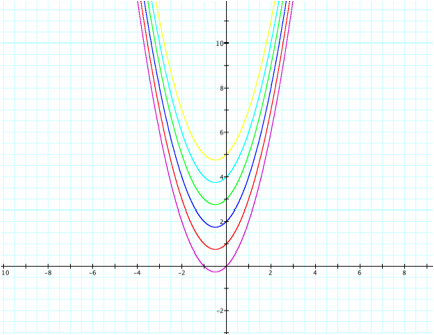
Now
we will investigate what happens to the parabola as we change the linear
term. I will keep the quadratic term
coefficient as one and for simplicity, make the constant term zero.
a
= 1, b = -5...0, c = 0
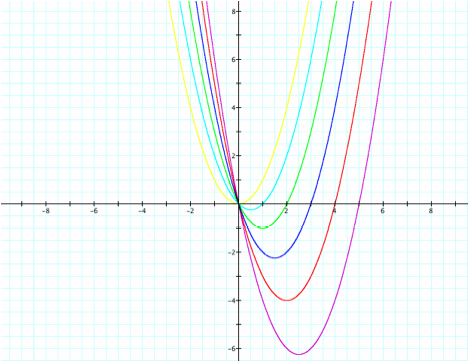
As
you can see, the linear term affects the position of the vertex (horizontally
and vertically). However, as b decreases, contrary to what one would
think, the vertex translates horizontally to the right and also translates
vertically in an upward direction.
a
= 1, b = 0...5, c = 0
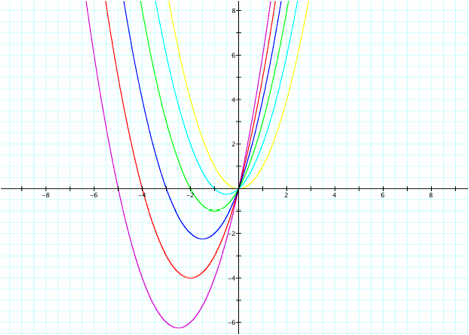
As
b increases, the vertex of the
parabola translates to the left also translates in a downward motion.
Furthermore, the translations of the parabola are reflections across the y-axis.
Now
we will investigate what happens to the parabola as we change the quadratic
coefficient and keep the linear and constant terms zero (again, for
simplicity).
a
= -5...0, b = 0, c = 0
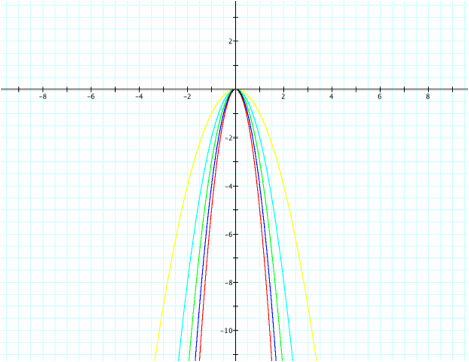
First
of all, we can clearly see that the parabola has been reflected across the x-axis. This is a result of the negative coefficient. Secondly, the parabolas “shrink” as a decreases. For instance, a = -5 is “wide” compared to a
= -2. Obviously for a = 0 the equation would become y = 0. This coefficient determines whether the parabola is
vertically compressed or stretched.
a
= 1...5, b = 0, c = 0
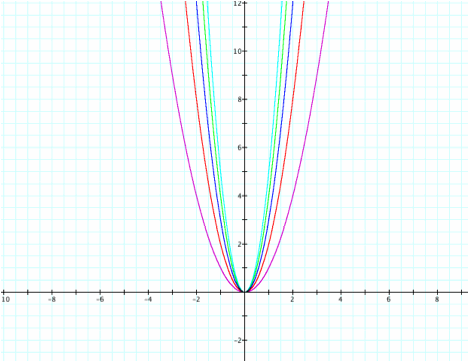
For
a values
of 1 through 5, the parabola “shrinks” as a
increases. Please note that the
vertex of these parabolas has been at the origin since the coefficient of the
quadratic term does not influence the location of the vertex, but only the
width of the parabola.