
Carisa Lindsay
Assignment 3
Locus of Parabolas
For quadratic
equations in standard form y=ax2+bx+c, we can explore what
happens to the parabola as we change the values of a, b, and c.
If we maintain a and c a constant of one,
and use the integer values -3<b<3, we can see that the parabolas
intersect at (0, 1).
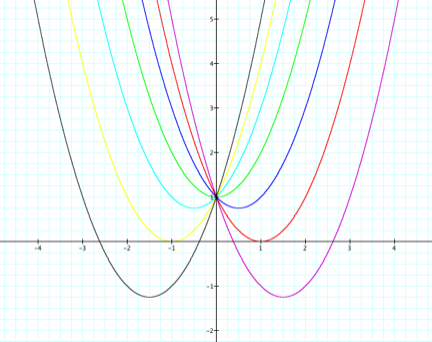
Furthermore, the
locus of vertices lies on the parabola y = -x2-1
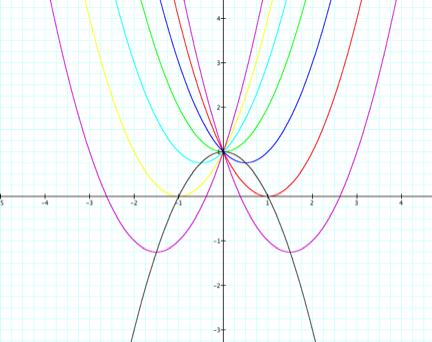
Now, we can
investigate what happens when we use c = 2.
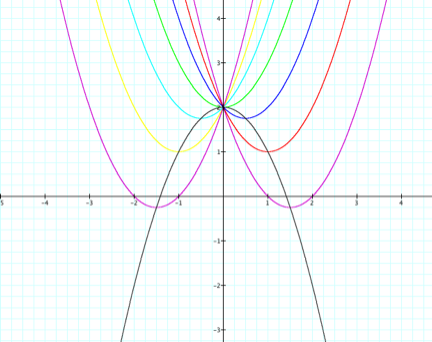
Notice that we have
the same pattern with the parabolas except we have shifted them all so that the
intersection is now (0, 2). This
includes the parabola which lies on the locus of vertices- the
equation of this
parabola is y
= -x2
+2.
We can generalize
this for various values of c.
Perhaps we can consider the values of c for -5<c<5.
In the following
animation, we can see for these various values of c, the locus of all of
these parabolas travels along the y-axis with the parabolas. Changing the values of c causes a vertical
translation of the parabolas.