
Carisa
Lindsay
Assignment
4
Centroids
of Triangles
First,
the question that begs to be asked, what is a centroid? A centroid of the circle is defined as the
intersection of all three medians of a triangle.
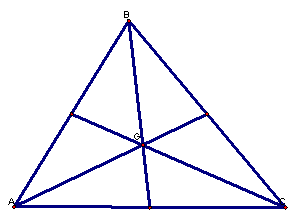
What
would happen if we used an obtuse triangle rather than an acute triangle?
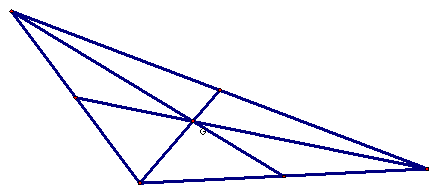
You
may notice that the centroid is still in approximately the same location- the
middle. Furthermore, the centroid is
still inside the triangle. We can also
predict that the centroid will remain inside the triangle for an equilateral
triangle.
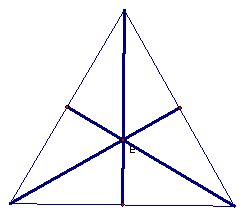
Equilateral
triangles are of special interest because the centroid is in the same place as
all of the other types of centers: the orthocenter, the circumcenter,
and the incenter.
We
can also easily show that the centroid divides each median into a ratio of 2:1
with an equilateral triangle.
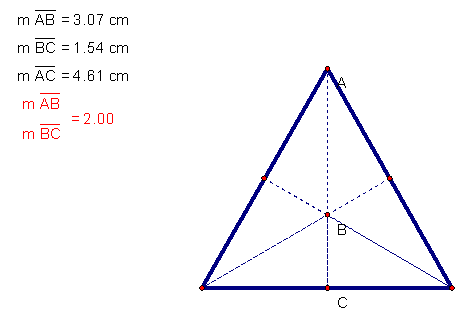
We
can also see the medians divide the equilateral triangle into three congruent
triangles.
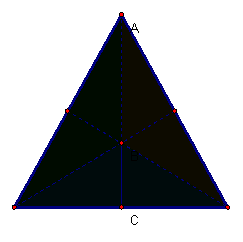
More
specifically, the apothem bisects the triangle into three 30-60-90 triangles.
As we know,
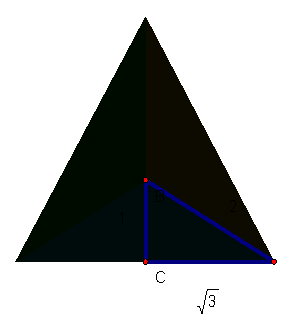
Based
on these congruent triangles, we know the length of BD is also 2. Now, we have our ratio of 2:1.
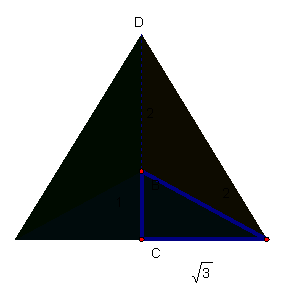
Perhaps
we should also consider isosceles triangles.
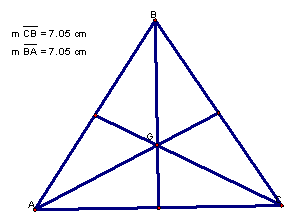
The
centroid again remains within the boundary of the sides of the triangle.
Why
are centroids important? Centroids are
most useful for studying centers of gravity and moments of inertia in physics
and engineering. So, it seems logical
that the centroid should remain within the triangle; only irregular shapes with
extended sides have centers of gravity on the exterior.