Carisa
Lindsay
Assignment
6
Comparing
Medial Triangles of Equilateral, Isosceles, and Right Triangles
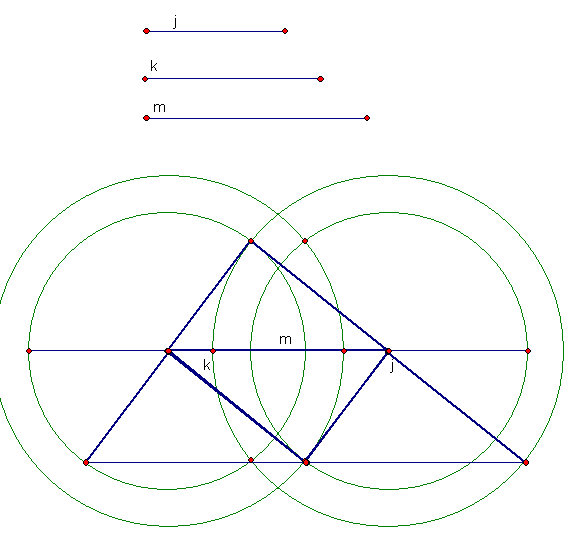
If
a triangle is an equilateral triangle, then the triangle formed by the midpoints
is also an equilateral triangle.
But,
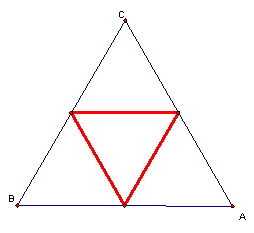
what can we conclude about triangles other than equilateral triangles?† Letís explore this idea with isosceles
triangles.
As
we can see, the medial triangle formed from an isosceles triangle is also an
isosceles triangle.
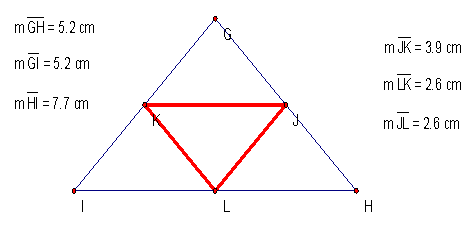
What
about right triangles?

Again, we see the medial
triangle formed from a right triangle is also a right triangle.
For
an arbitrary triangle, we can construct the triangle formed by the
medians.†

Given
triangle DEF with midpoints A, B, and C, we know segment AB is parallel to EF
by the Midsegment Theorem.† Furthermore,
we know BC is parallel to DE for the same reason; and AC is also parallel to
DF.† Since the medial is constructed from
the midpoints of each side of the triangle, we also know that each side is half
its length.† Therefore, the medial
triangle formed is similar since the side lengths are proportional.
Unfinished
write-up: