
Carisa
Lindsay
Assignment
#8:
Exploring
Altitudes and Orthocenters
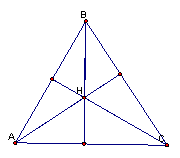
First,
in order to construct the orthocenter for ∆ABC, construct the altitudes
for each vertex of the triangle. The
intersection of these altitudes is the orthocenter.
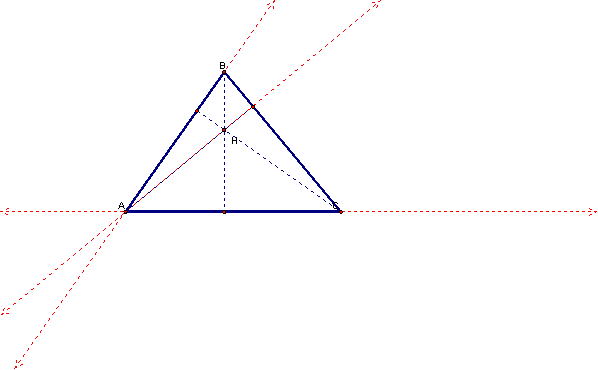
Now, we can construct the orthocenter for
∆HBC in a similar way by finding the intersection of the altitudes. As it turns out, this intersection is Point
A.
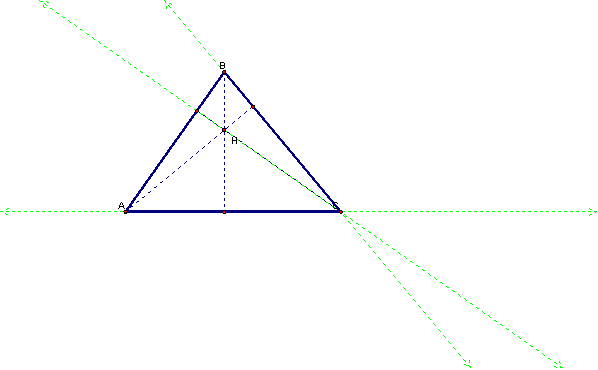
Now, we can construct the orthocenter for
∆HAB similarly and see that the orthocenter is Point C.

Lastly, we can construct the final
orthocenter for ∆HAC and see the intersection of altitudes is Point B.
Next, we can construct the circumcircles for
each triangle.

What kinds of observations can we make if we
construct the nine-point circles around each triangle?

We can see through this construction of the
nine-point circle for ABC that the orthocenters
align.