
Carisa Lindsay
EMAT 6690
Conic Sections
What is a conic
section? A conic section is the result of a plane intersecting various parts of
two cones essentially stacked on top of each other (slightly hourglass in
shape). Depending upon where the plane
intersects the cones, the result will be one of four possibilities: a circle,
an ellipse, a parabola, or a hyperbola.
All of these shapes have similar characteristics yet have vastly
different appearances.
A circle:
![]()


To see an animation
of a double cone with the plane z=1, click here.
An ellipse:



To see an animation
of a double cone with the plane y=2z+1, click here.
A parabola:
![]()


To see an animation
of a double cone with the plane z=x-2, click here.
A hyperbola:



To see an animation
of a double cone with the plane y=1, click here
So how are these
figures constructed? All of these
figures are geometrically sound are based upon foci and equidistant line
segments.
The circle is the
simplest construction since by definition, the circle
is the locus of points equidistant from the center.
Click here for a GSP demonstration.
A parabola is
slightly more difficult to construct, but is also based upon the same
principle.
We must first
construct the directrix line and a focus. Then, we
can construct a point on the directrix and draw a
line segment from this point to the focus.
Once we have the line segment, we can construct the perpendicular
bisector. The intersection of the
perpendicular bisector with the perpendicular line from the point on the directrix will ultimately be the point to create the
parabola.
Click here for a GSP demonstration.
An ellipse can be
constructed from two foci with their sum of the distances being constant as
point P travels through the ellipse. We can again construct this using
GSP. First, we must construct an
arbitrary circle and two foci- one of which is the center of the circle and the
other somewhere within the bounds of the interior of the circle. We can construct a line from the center to an
arbitrary point on the circle and then construct a line segment from this
arbitrary point to the other focus.
Their intersection will create an ellipse since these two distances’ sum
will be constant.
Click here for a GSP demonstration.
A hyperbola has a
similar construction as the ellipse- the major difference is the presence of
one of the foci being located on the exterior of the initial circle. We will again create an arbitrary circle with
two foci (one as the center and one lying outside of the circle). Much like the ellipse, we will construct a
line from the center to an arbitrary point on the circle and then construct a
line segment from this point to the other focus. Their intersection will create a hyperbola.
Click here for a GSP demonstration.
So how do we go from
these geometric figures to complex algebraic equations?
There’s a reason why
the textbooks leave this out because we end up with some awful equations!
Let’s first consider
the equation of a double cone.


In order to construct
a circle, we know we need a plane that is parallel to the x-y plane. So z=d,
where d is any real number.

Visually, it is easy
to see how these two combined can create the conic section of a circle.
Through simple
substitution, we can arrive at the standard equation of a circle given the
equation of the double cone.
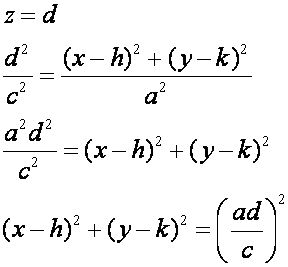
The derivation of an
ellipse is not quite as simple.
We know that we need
a plane that comes in at an angle to the z-axis, so the equation should have
“slope” for a lack of a better term.
So, we can say that
the general equation of the plane to create an ellipse should be y=mz+b. However, due to the complexity of this problem, I
will use the equation y=2z+1.

When I attempted this
problem for the general case, the problem became a challenge for the completing
the square step and I had difficulty getting the problem to become standard form for the ellipse.

Through a similar
process, we can see how the parabola can be derived from these basic
equations. Again, we need an equation
with “tilt” or some kind of “slope”, but through the x-z plane. So we can use z=mx+b
as a general equation. Much like the
ellipse, these calculations are quite tedious!

Lastly, we can see
how a hyperbola can be derived. This
time, we need a plane that is perpendicular to the x-y plane, we can use y=d,
again where d is any real number.

 ß Standard Equation of a hyperbola
ß Standard Equation of a hyperbola