Carisa Lindsay

EMAT 6690

Logarithmic Functions

Logarithmic functions are essentially just inverses of exponential functions. This is how we are often taught in school, but there is seldom any further investigation as to why this is true. Students are simply told that this is how it is.

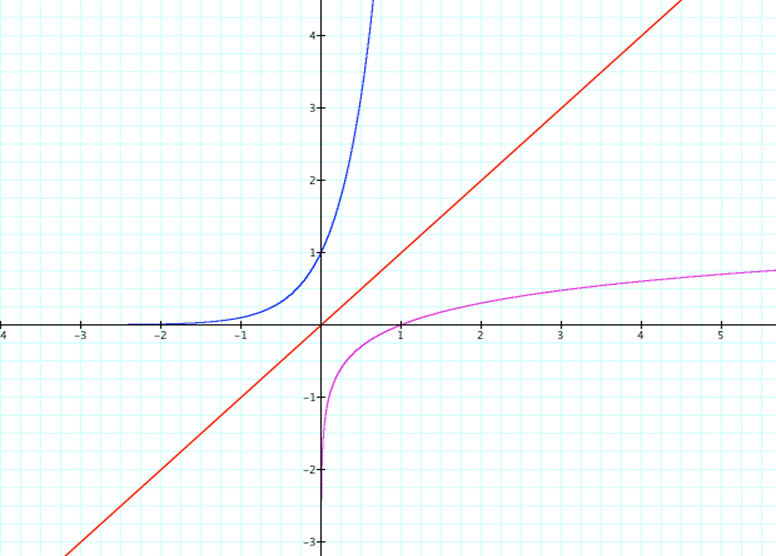
As you can see in the above graphic, logarithms are truly inverses of exponential functions since it is a reflection over the line y=x.

Logarithmic functions behave in similar ways as our more familiar functions do- we can stretch, compress, reflect, and translate them.

For instance,

y=2*log x

will yield a result of the parent function vertically stretched by a factor of 2.

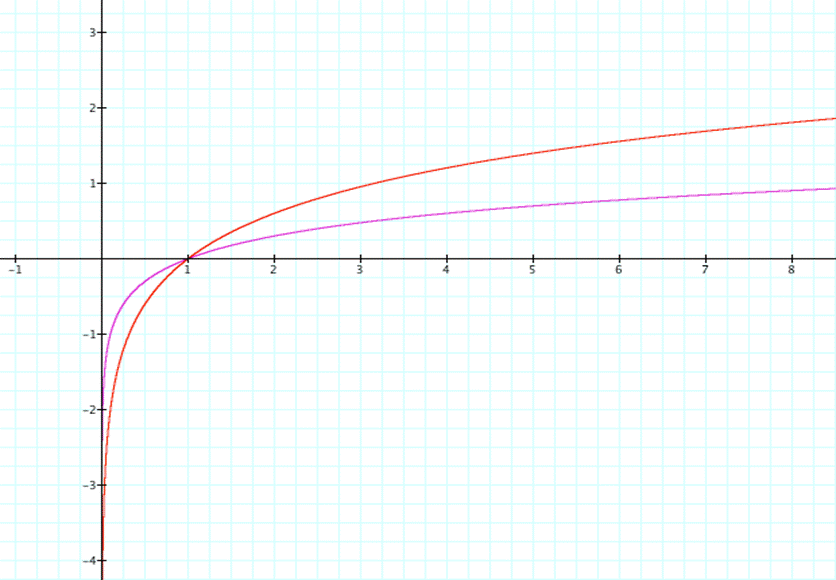
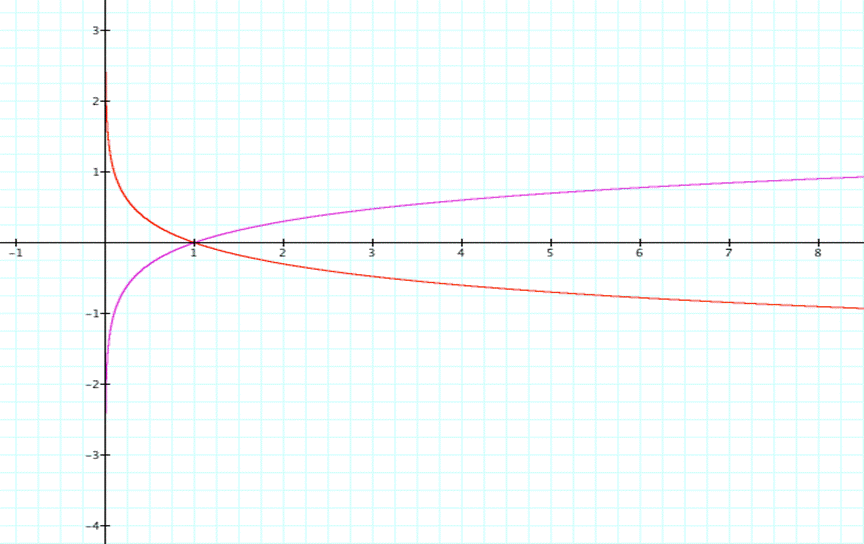
We will see a similar result for reflections and translations:

y=-log x

y=log(x+3)

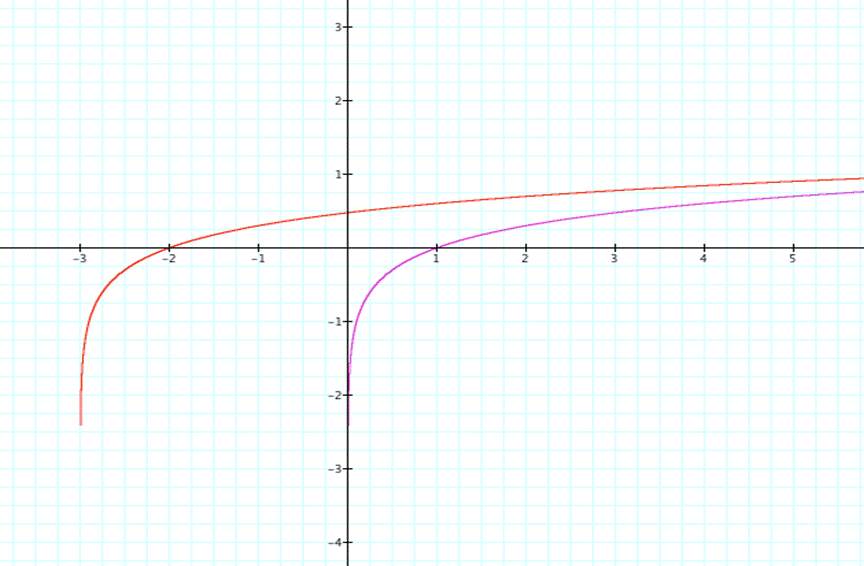
The domain of Logarithmic Functions

As you can see on the following graphs, which has not been horizontally translated, the lowest defined value of the logarithmic function is 0.

The domain will continue onto infinity (we can verify this through testing various points and make assumptions about the end behavior).

So far, we have focused primarily on logarithms with a base of 10. What happens if we change the base? How are the graphs similar? Different?

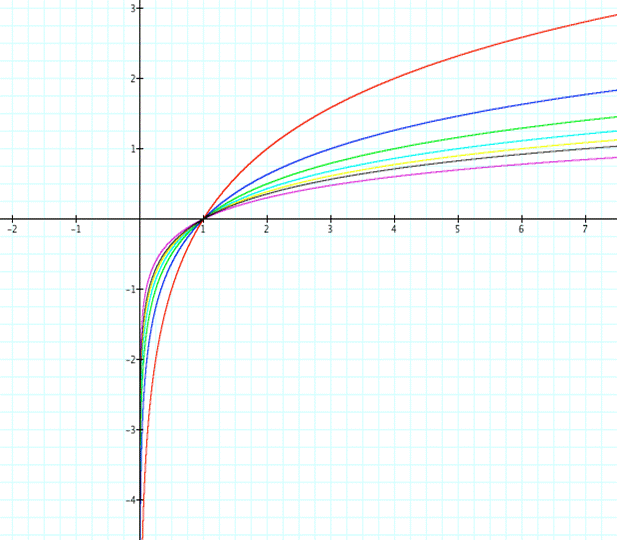
If we consider simple logarithms free of transformations, we can clearly see the effect the base will have on the graph. Essentially, as we increase the base number, the less steep it becomes. It appears that the growth changes less steadily as the base increases. We also notice that all of the logarithms have a common point of intersection, (1,0). This is not surprising since the log of 1 is always zero.

Click here to see an animation.

You may wonder, what is happening for values less than one? It seems to be inverting itself as the base becomes less than one. Let’s take a closer look.

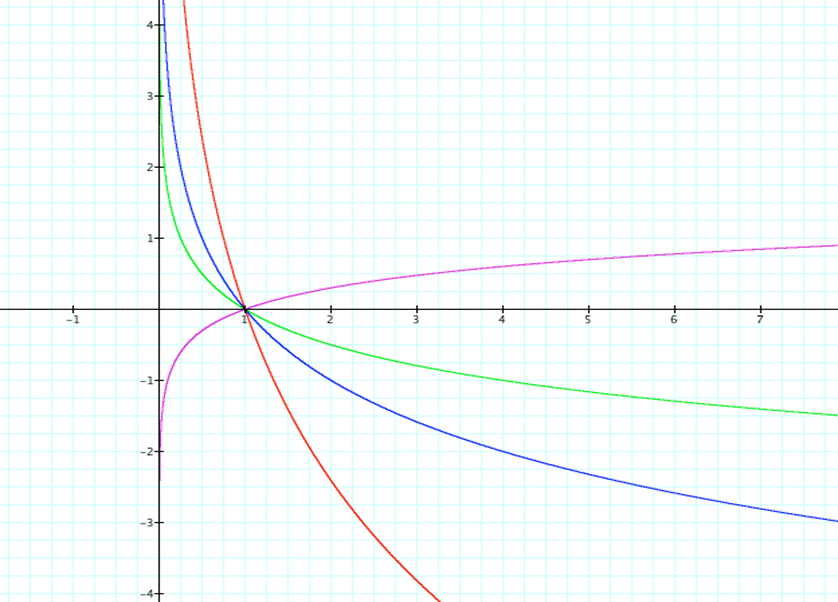
WE need the definition of a logarithm to help us explain why this occurs. Remember, logarithms are simply inverses of exponential functions. The logarithms we have looked at so far have looked like exponential growth. With rational base values, we seem to experience something like exponential decay. Let’s convert our logarithms to exponential form to see if they truly are examples of exponential decay.

y =log_0.75 (x) à (0.75)^y = x

Since our base value is less than one, we know the graph exhibits exponential decay. The base of the logarithm is essentially the base of the exponent, so all of our rational bases will be examples of exponential decay. For the same reason, our bases greater than one will have an exponential growth pattern.

What about values less than one?

For base values less than one, we have undefined values.

What are logarithms useful for?

Logarithmic functions are especially useful to us to approximate and apply to fields other than mathematics.

Logarithms are mostly taught through solving interest problems as a means of solving an exponential equation. They can also be used for solving various mortgage problems (since they are similar to interest problems).

We can also use logarithms to solve population problems and predict population growth as well as radioactive decay.

Logarithms are also used with earthquake magnitude. The Richter scale is based on base 10, so we can use logarithms to solve for unknown quantities.

Chemists also use logarithms when discussing the pH of various substances when determining the acidity or how basic the substance is.

Logarithms can also be used for determining the intensity of sound (volume). The decibel scale is essentially exponential and therefore logarithmic also.

Click here to return to Lindsay’s homepage