Carisa
Lindsay
EMAT
6690
Polynomial
Exploration
While
polynomials may seem very different on the surface, we can see through various
explorations that they exert many similar characteristics.
For
instance, we can see that polynomials of even degree have similar end behavior
and follow a pattern which allows us to predict what higher powered polynomials
will resemble. In the following
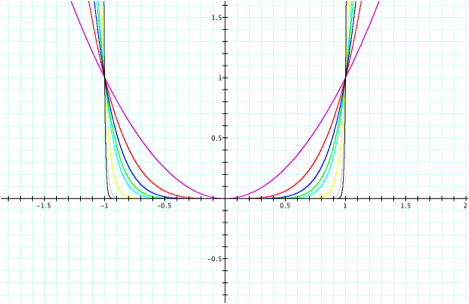
graphic, we can see as the degree increases, the midsection ÒflattensÓ. This is the most obvious difference
between the polynomials. We can
also see the locus of points for all of these polynomials have common points of
(1,1) and (-1, 1). You might ask
why this is the case. If we
perform the inverse operation of any even-degree polynomial in order to solve
for a particular value, we can see the nth root of 1 is always 1 or -1. This explains the common points. However, we can also see, for positive
coefficients, the end behavior is rising on both sides towards positive
infinity.
How do we know the end behavior is increasing towards
positive infinity? How do we know
the graph will never come back towards the x-axis?
The
best way to satisfy this curiosity is to test points. We should be able to pick any arbitrary point,
magnitude irrelevant, and see the direct relationship (as one variable
increases, so does the other). For
instance, letÕs consider x=1,692 and substitute it in for y=x^4. We yield y= and see when x is a large
number, y is even larger.
This makes sense since a number to a power will yield a result much
larger than itself. Perhaps you
ask, what about really small numbers, such as negative values? Think about what happens when you raise
a negative number to an even power- the result is always positive. We can safely conclude that polynomials
of even-degree will always increase towards positive infinity.
What happens when we have a negative leading coefficient?
We
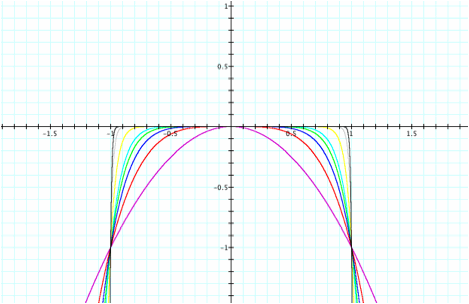
see a similar behavior to the positive leading coefficient except the graph has
been reflected across the x-axis.
We see the graphs still ÒflattenÓ as the degree increases and we have
common points which are reflected along with the graph. We the locus of points are now located
at points (1, -1) and (-1, -1).
This happens for the same reason as above, but now there is a negative sign
preceding.
What happens to the even degree polynomials if we make
the coefficient a number other than 1?
LetÕs
consider a coefficient of 2. In the following example, I am only comparing
y=x^2 for simplicity sake.
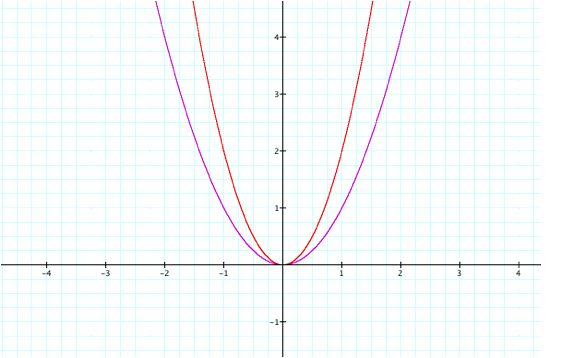
As
you can see, the basic shape and end behavior of the polynomial has not
changed. What has changed? We can see the major difference is how
much the graph has ÒshrunkÓ. It
seems that it is ÒskinnierÓ than the original. Furthermore, y=2x^2 is half the size of y=x^2, or it has
been vertically stretched by a factor of 2. Because all even-powered polynomials behave in a similar
fashion, we can conclude that we would see similar results with yx^4, y=x^6,
etc.
What
about coefficients higher than two?
What do you think will happen to the graph?
LetÕs
try a coefficient of 10.
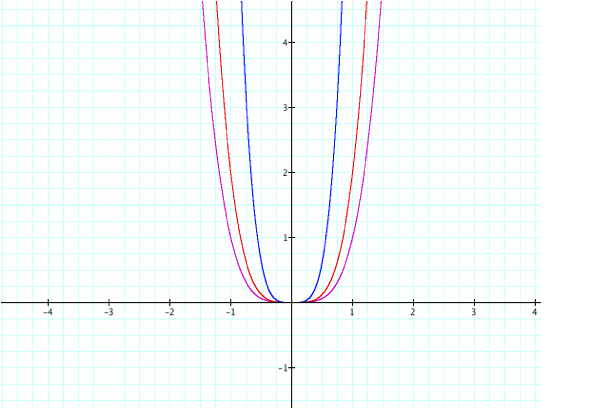
The
pink line represents y=x^4, red is y=2x^4, and blue is y=10x^4. As you can see, even with other
even-degreed polynomials, the larger the coefficient, the ÒskinnierÓ the graph
becomes. This makes sense because
we are now stretching the graph vertically by a factor of 10 this time instead
of 2.
LetÕs
consider polynomials of odd-degree.
Again, we can see that odd-degree polynomials exhibit similar
characteristics to each other and we can predict what higher degree polynomials
will look like.
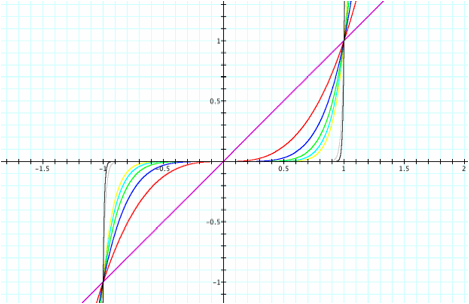
Unlike
the even degree polynomials, we see end behavior in opposing directions. The left side of the polynomial
decreases towards negative infinity while the right side increases towards
positive infinity. Much like the
even degree polynomials, we see the locus of points for all odd-degree
polynomials have common points of (1,1) but instead (-1,-1). The reason the common point changes to
(-1, -1) is because the nth root of -1 is -1 for all odd
roots.
How do we know the end behavior ÒbehavesÓ like this all
the time and not return to the x-axis?
Much
like the even-degree behavior, we should test points. Much like the even degreed polynomial, if we select an
arbitrary number and substitute the value into y=x^3, we will again see a
direct relationship. As the value
of x increases, the value of y will also increase. Furthermore, the smaller the value of x, the smaller the
value of y will become. For
instance, letÕs consider x=-4. If
we (-4)^3, we get an even smaller result of -64. While this is not a proof, we can safely assume any real
number will also exhibit this quality.
What happens when we have a negative leading coefficient
in odd-degree plynomials?
We
see a similar trend as the even degree polynomial with a negative leading
coefficient. It too has been reflected across the x-axis and the common locus of points have also been reflected. The common points are now (1, -1) and
(-1, 1) since the negative preceding affects the final outcome. The end behavior on an odd degree
polynomial with a negative leading coefficient has the left side increasing
towards positive infinity while the right side is now decreasing towards
negative infinity.
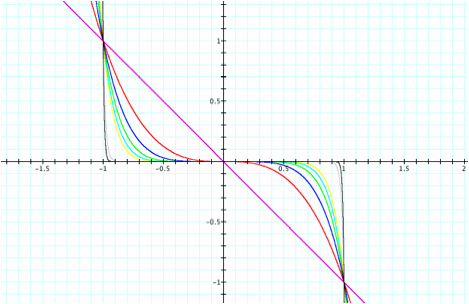
What happens to odd degree polynomials when the
coefficient is a number other than 1?
Much
like the even-degreed polynomials, we should similar results. The coefficient should only affect the
stretch or compression of the graph, but not the end behavior. LetÕs first investigate a coefficient
of 3.
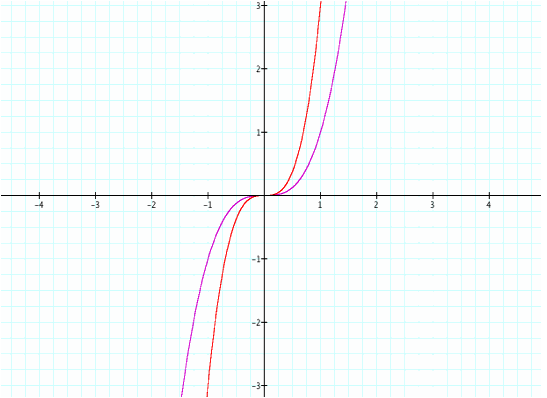
Again,
we see y=3x^3 (red line) is seemingly ÒskinnierÓ and has been vertically
stretched by a factor of 3. We
should see a similar trend for larger coefficients. For instance, let the coefficient be 10 again.
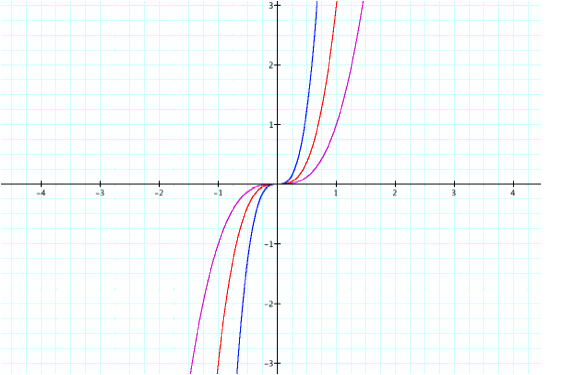
We
see that we were exactly right.
Y=10x^3 (blue line) is even ÒskinnierÓ, or vertically stretched by a
factor of 10.
We
have now thoroughly explored various values of possible leading coefficients
for even and odd degree polynomials.
Perhaps we should consider how the coefficients of the following terms
affect the behavior of the graph.
What do you think the middle terms control?
To
find out, letÕs keep the leading coefficient a constant one and the constant
term zero.
Again,
letÕs first consider even-degreed polynomials.
The
following graph represents y=x^2 (pink), y=x^2+x (red), and y=x^2+3x
(blue). We can see that the middle
term affects the location of the vertex, but does not stretch or compress the
parabola.
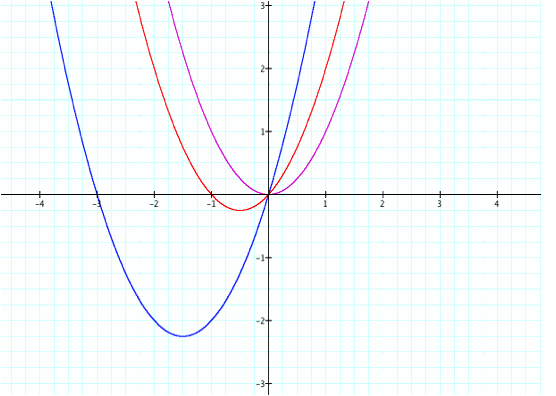
How does the sign of the middle term affect the
graph?
LetÕs
consider y=x^2 (pink), y=x^2-x (red), and y=x^2-3x (blue):
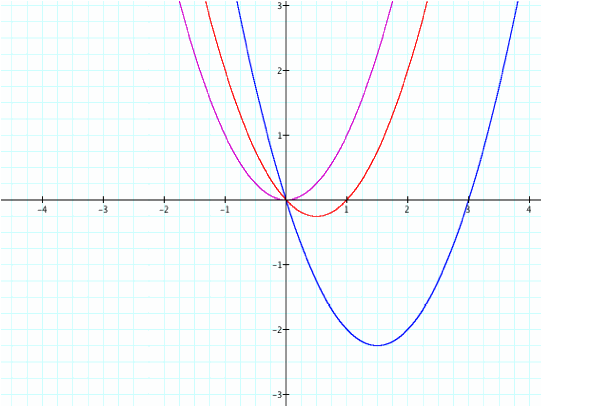
The
middle term seems to have the opposite effect and translate the vertex left for
positive values and right for negative values. Is this true for higher order polynomials? LetÕs consider y=x^10, y=x^10-x,
y=x^10-3x:
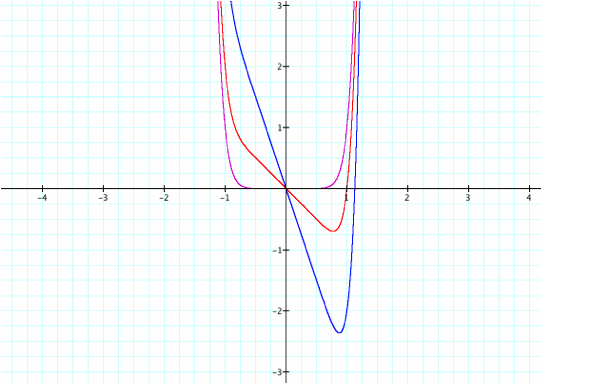
Again,
this middle term affects the location of the vertex in a somewhat opposing
manner.
LetÕs
briefly look at odd-degreed polynomials.
We
can see a similar effect of the next middle term with these polynomials:
Y=x^3
(pink), y=x^3-x^2 (red), y=x^3-3x^2(blue)
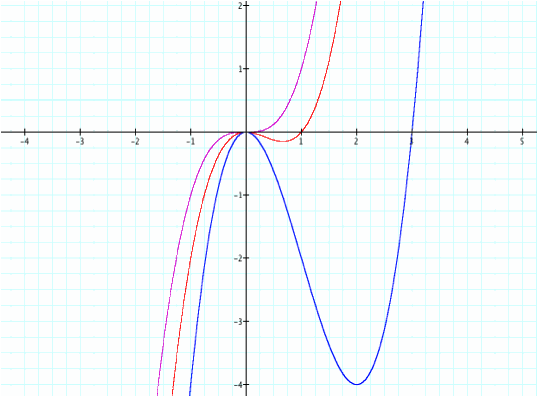
y=x^3
(pink), y=x^3+x^2 (red), y=x^3+3x^2 (blue)
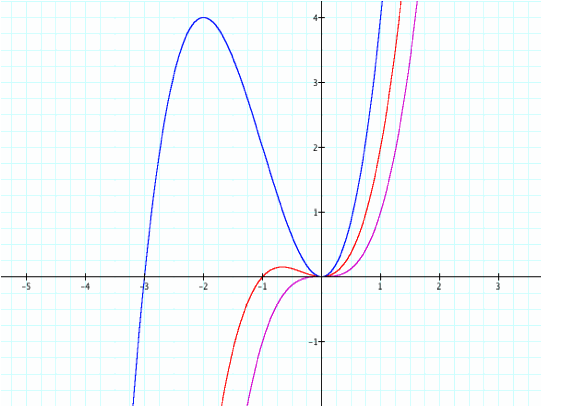
With
odd-degreed polynomials, we can see the next middle term effects the graph by
translating one of the ÒhillsÓ and making the ÒhillÓ much steeper.
If
we again look at a cubic polynomial, what happens if the quadratic term remains
constant, but instead the linear term changes?
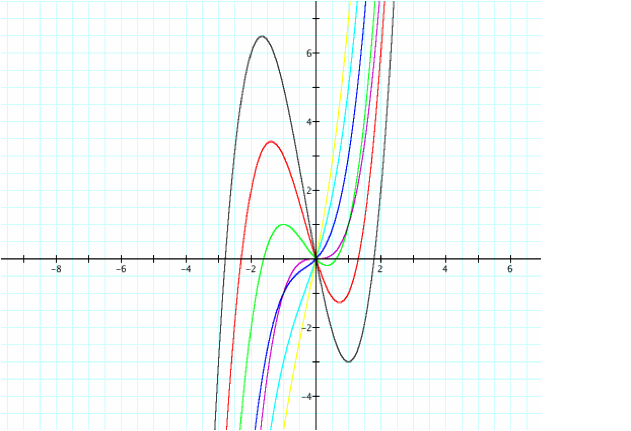
As
you can see, the linear term has a similar effect on the cubic graph as the
quadratic term. It too affects how
large the ÒhillsÓ and ÒvalleysÓ of the cubic polynomial become. Essentially, the larger the linear
coefficient becomes, the ÒstraighterÓ the cubic function appears to be. This includes the assumption that
negative coefficients are considered to be ÒsmallÓ numbers. The charcoal gray equation has the most
significant valleys and also has the smallest linear coefficient value
(y=x^3+x^2-5x). The ÒstraightestÓ
cubic equation appears to be the yellow equation and it has the largest linear
coefficient (y=x^3+x^2+5x).
What conclusions can we make about the final constant
term?
The
final constant term has n roots which are all factors
of the constant term. This is
because (x-x1)(x-x2)(x-x3)É(x-xn) expanded will
become an nth degree polynomial and constant x1x2x3Éxn.
Suppose
we have a simple cubic polynomial y=(x-1)(x-2)(x-3). Since this cubic is in factored form, we know the roots are
x=1, 2, and 3. If we expand this
cubic, we yield a result of y=x^3-6x^2+11x-6. As you can see, the constant term of the expanded form is
the same as the product of factors.
We
can consider a similar quartic polynomial
problem. Suppose y= 
; so the roots would be x=-4, 3, -2, and -5. The expanded form yields 
. Again, we can see the product of the
factors matches the constant term.
This makes sense because using the distributive property would have us
multiplying the last terms of each factor.
What happens when we add polynomials together? Will the result also be a
polynomial? Why or why not?
If
we add two polynomials of the same degree, we will of course get another
polynomial. This is because
we are simply combining like terms and changing the shape of the polynomial
(stretch or compression, possibly a reflection). When the polynomials are of the same degree, we are not
drastically changing the exponents or x
so that it would no longer be a polynomial (for instance, adding polynomials
will not involve taking the square root of x). If we add polynomials of different
degrees, we will still result in a polynomial, but it likely to take the shape
of the higher power. For instance:
f(x)= 3x^2-x+2
and g(x)=3x^5+4x^2-1
f(x)+g(x)
will yield a quintic polynomial. See below:
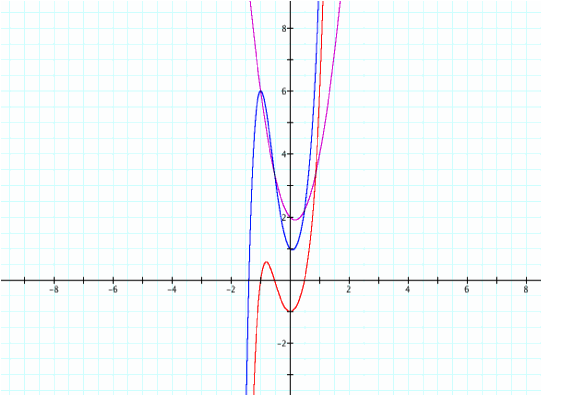
The
blue function bears resemblance to the higher-degreed polynomial (in this case,
g(x)).
Is the product of polynomials a polynomial? Why or why not?
The
product of polynomials should yield a result of a higher-powered
polynomial. Using the laws of
exponents, when multiplying polynomials we are simply adding the exponents
(using the product rule).
Regardless of the polynomial, we should always maintain whole numbers as
the exponents. This can quickly
become a tedious manipulation due to complicated distributing, so letÕs consider
a simple example:
f(x)=x^4 and g(x)=3x^7
f
x g (x)=3x^4+7=3x^11
The
exponent is still a positive whole number, and therefore still meets the
qualifications of being a polynomial.
Does the quotient of polynomials yield always yield a
polynomial?
No,
we can see using one such example, we can see through
long division that the quotient involves a remainder. The remainder is not a polynomial. However, the remainder is
an example of a rational function.
A rational function is defined as the quotient of two polynomial
functions.
What can we use polynomials for? Why are they important?
Many
phenomena in the universe are best-fit using polynomials. Given the simplicity of polynomials and
the nice curves they produce, they are ideal for approximating other more
complex functions. If we are able
to approximate these functions, then we can in turn make predictions about
these particular phenomena and apply it.
What is the significance of the degree of a polynomial
and how can we determine the number of roots a polynomial has based on the
degree?
Through
the Fundamental Theorem of Algebra, we can determine the number of roots a
polynomial has. This theorem tells
us that polynomial of nth degree has no more than n roots (real or complex) and
must have at least one complex root.
Generally speaking, a linear polynomial would have one root, a quadratic
would have two roots, a cubic would have three roots, and so on.
Continuity/Differentiation
Polynomials
are particularly ÒniceÓ because they lack holes and asymptotes
(ÒdiscontinuitiesÓ). Every point
along the graph is differentiable (we are able to find the tangent line at
every point). Furthermore, we are
able to integrate just as ÒnicelyÓ and approximate the area under the
curves. This is precisely why
polynomials are the choice of many scientists to predict behavior of various
phenomena.