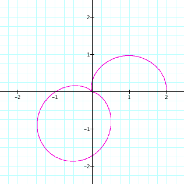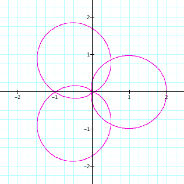Exploring Polar Equations: n-Leaf Roses

By: Laura Lowe

Problem: Investigate r = a + b cos(kq)

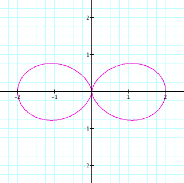
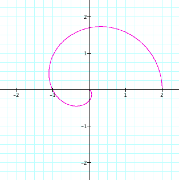
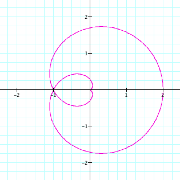
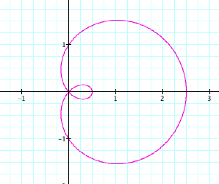
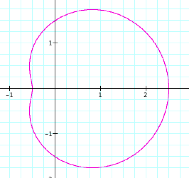
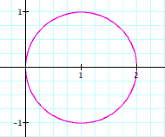
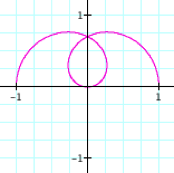
We begin by graphing r = a + b cos(kq) with a = 1, b = 1, k = 1, and 0 < q < 2p.

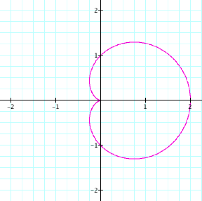
This is an interesting graph, but what if we hold a = 1, b = 1, and 0 < q < 2p and let k vary? (We will restrict a, b, and k to be positive rational numbers greater than 1.)

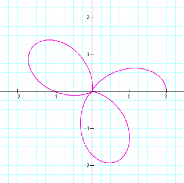
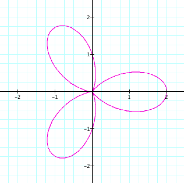
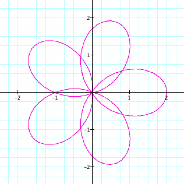
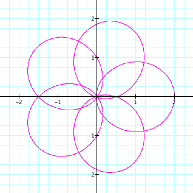
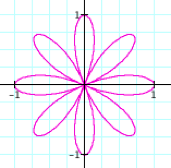
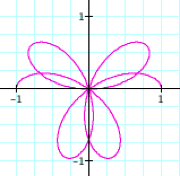
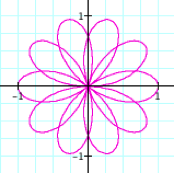
k = 2	k = 3
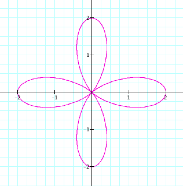
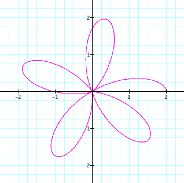
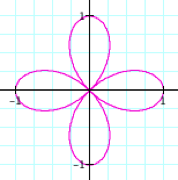
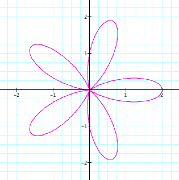
k = 4	k = 5

It appears that k, a natural number, dictates the number of loops (called leaves)in the figure. If k = 7, there should be 7 leaves. Try it and see.

Now that we have a conjecture when k is a natural number, what about when k is rational? Logically, we would expect to get partial leaves. Let’s try a few.

k = ½	k = 3/2
k = 5/2	k = 7/2

\We did get partial leaves, but it looks like the pattern may continue if we make q larger. Let’s try letting 0 < q < 4p.

k = ½	k = 3/2
k = 5/2	k = 7/2

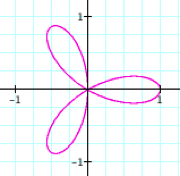
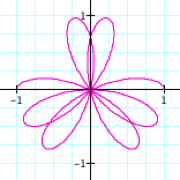
If we suppose k = c/d where c and d are natural numbers, it appears that the graphs have c leaves when we let 0 < q < 2dp. Let’s try a few.

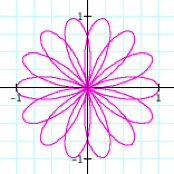
0 < q < 6p	0 < q < 8p

It appears our conjecture is true.

In fact when a and b are equal (but not 0) these properties still hold. The only difference is the relative size of the rose.

Now let’s look at the graph when we hold a =1 and k = 1and let b vary.

b = 2	b = 3
b = 4	b = 5

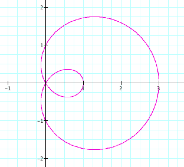
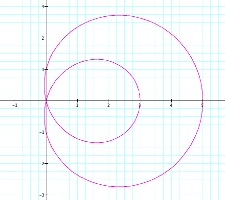
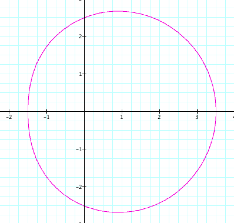
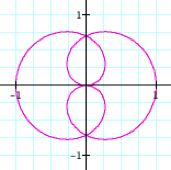
It appears that as be increases, the graph becomes a circular figure with an outer loop intersecting the x-axis at x = 0 and x = b +1, and the inner loop intersecting the x-axis at x = 0 and x = b – 1. At the same time the y-intercepts remain at y = ±1. So we would expect that when b = 6, then the outer loop would intersect at x = 0 and x = 7 and the inner loop at x = 0 and x = 5. Try this and see.

Again, we have a conjecture when b is a natural number, so what about when b is rational? Since b appears only to affect the “size” of the loops, we would not expect this to change when b is rational. Let’s try a few.

b = 3/2	b = 5/2

Again it appears our conjecture is true.

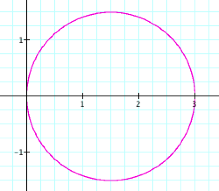
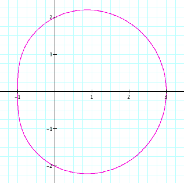
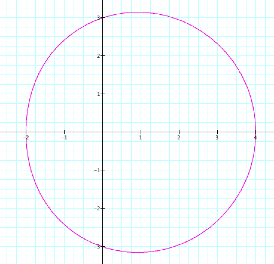
Now let’s look at the graph when we hold b =1 and k = 1and let a vary.

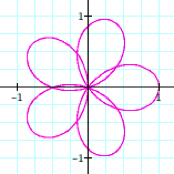
a = 2

a = 3

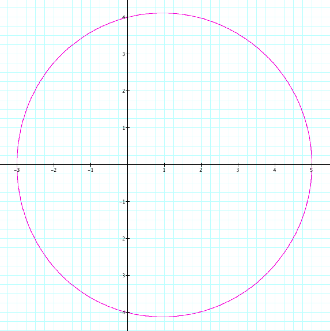
a = 4

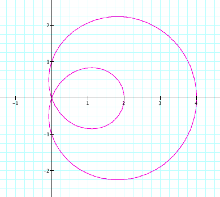
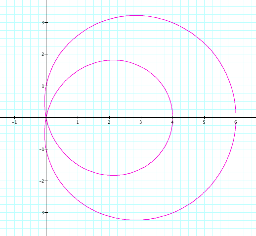
It appears that as a increases, the graph becomes more and more circular with x-intercepts x = a + 1 and x = -a +1, and y-intercepts y = ±a. So when a = 6, we would expect our x-intercepts to be x = -5 and x = 7 and y-intercepts to be y = -6 and y = 6. Try this and see.

Again, we have a conjecture when a is a natural number, so what about when a is rational? Since a appears only to affect the “size” of the circular figure, we would not expect this to change when a is rational. Let’s try a few.

a = 3/2

a = 5/2

Again it appears our conjecture is true.

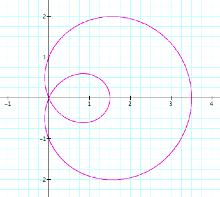
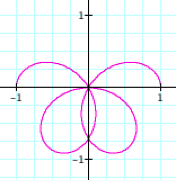
Now let’s compare these graphs to the graphs of r = bcos(kq). To begin we will let b = 1, k = 1, and 0 < q < 2p.

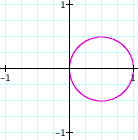
From our earlier explorations we can expect that if we hold k = 1 constant, and let b vary, the graph should remain a circle only bigger.

b = 2

b = 3

Now what if we hold b = 1 constant and let k vary we should expect, from our earlier explorations, that k will dictate the number of leaves in the rose.

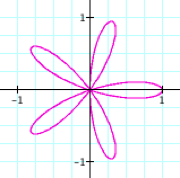
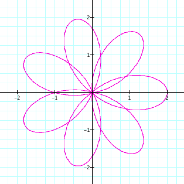
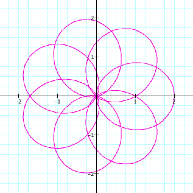
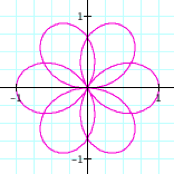
k = 2	k = 3
k = 4	k = 5

This is interesting. Now, when k is even, we have 2k leaves on the rose, but when n is odd we only have k leaves on the rose. Let’s see what happens when k is rational.

k = ½	k = 3/2
k = 5/2	k = 7/2

Again, we got partial leaves. When k = c/d the graph has c – 1full leaves and 2 half leaves. As we found earlier, we can guess that if we make q larger, we will see more leaves. Let 0 < q < 4p and graph.

k = ½	k = 3/2
k = 5/2	k = 7/2

Now it appears that the graphs have 2c leaves when we let 0 < q < 2dp. Let’s try a few more and see if our conjecture holds.

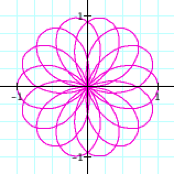
0 < q < 6p	0 < q < 8p

Another interesting result. This time, when c is odd and d is odd there are c leaves, and when c is odd and d is even, there are 2c leaves. What if c even and d is odd? Let’s try , with 0 < q < 6p. (We will disregard the case of c and d both even, as it it will reduce to one of the other cases.)

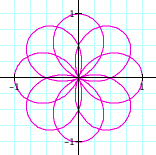
So when c is even and d is odd, there are 2c leaves. Try more examples and see if this result holds.

What if cos is replaced with sin in all of these? A quick check reveals that this only rotates the graph 90° counter-clockwise. Why? (Hint: Look to your unit circle.)

Extensions:

What happens when b or k are 0?

What happens when we let a, b, and k be negative?

Return