
Cooling Water
By: Laura Lowe
Problem: Use the following exploration to generate
a function to predict observed data.
a. Take a cup of hot water and measure its
initial temperature (time = 0) and then record temperature readings each minute
for 30 minutes. Make note of the room temperature . . .
b. Enter the data on a spread sheet and
construct a function that will model the data.
c. Using the function predict the temperature
after 45 minutes, 60 minutes, or 300 minutes.
d. Calculate a measure of the error between
your model and the observed data by taking the square of the difference for
each time, sum the squares, and divide by the number of data points. You can
use this statistic to guide refinement of your function to model the data.
I began by boiling water and
then pouring it into a coffee mug.
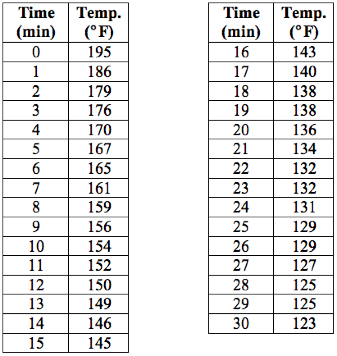
The room temperature was 72¡F. I used
my probe thermometer to measure the water temperature every minute for 30
minutes. My data was as follows:
After I collected the data I
used Microsoft Excel to plot the points on a scatterplot.
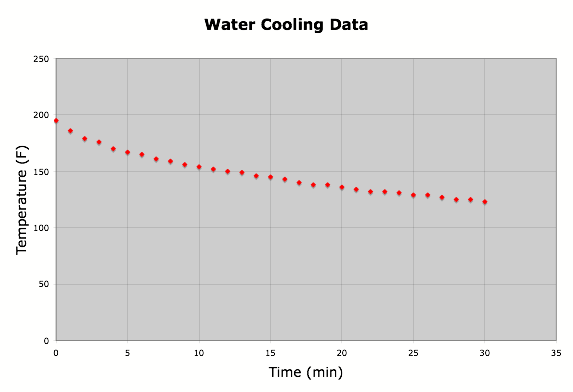
This data looks relatively
linear, but it also has a leveling off as time increases, so it could be
exponential decay.
I used Excel to find a linear
regression equation relating time and temperature. (Figure 1)

Figure 1
This looks like a pretty good
regression line. R2 is
very close to 1, which means r, the coefficient of correlation, is also very
close to 1. (r = 0.9695) In fact when I used Excel to average
the squared differences of the observed temperature and the predicted
temperature, I got 21.64. This is
a rather large error. It also
predicts a temperature of 86.2¡F in 45 minutes, 55.3¡F in 60 minutes, and -439.9¡F in 300 minutes. This just doesnÕt make sense when the room temperature is 72¡F. I
think we can do better.
Next I used Excel to find an
exponential regression equations relating time and temperature. (Figure 2)

Figure 2
This function does not look
any better than the linear equation.
R2 is slightly better (r = 0.9830), but when I used Excel to
average the squared differences of the observed temperature and the predicted
temperature, I got 14.49. Again,
this is better than the linear function.
However, this equation predicts a temperature of 97.5¡F in 45 minutes, 79.4¡F in 60 minutes, and 2.98¡F in 300 minutes. This is the same problem I ran into with the linear
function. There is no way the
water will reach 2.98¡F when the room is 72¡F. Now
what?
When I took a second look at
the regression equation Excel gave me, I can see the problem. Logically an exponential function of
the water temperature should have a horizontal asymptote y = 72, but the regression function in Excel assumes a
horizontal asymptote y = 0. I adjusted for this by subtracting 72
from each data point, and then having Excel find the exponential
regression. (Figure 3)
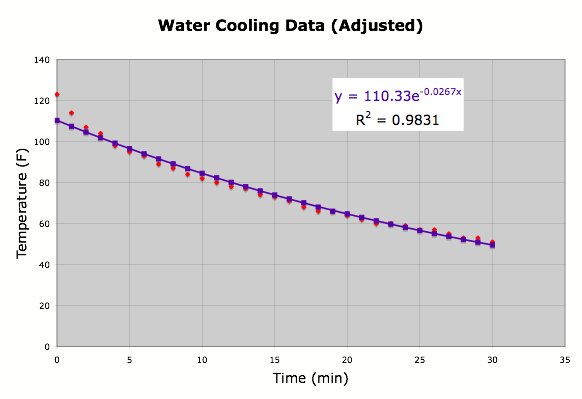
Figure 3
This looks better. Now I adjusted the equation by adding
72. So my regression equation
became y = 110.33e-0.0267x + 72.
This time when I used Excel to average the squared differences of the
observed temperature and the predicted temperature, I got 9.23. This equation predicts a temperature of
105.2¡F
in 45 minutes, 94.2¡F in 60 minutes, and 72.0¡F in 300 minutes. This makes a lot more sense.
After all this I concluded
that a good equation to predict the temperature of my water is:
![]()
(I also concluded that I need
to replace my thermometer.)
NewtonÕs Law
of Cooling
NewtonÕs Law of Cooling describes the cooling of a warmer object
to the cooler temperature of the environment. The formula is:
![]()
T(t) is the temperature of the object at
a time t
Te
is the constant
temperature of the environment
T0 is the initial
temperature of the object
k is a constant depending on the
properties of the object.
When
I applied this formula to my water, using (0, 195) and (30, 123) to find k, I found my equation should have been:
![]()
When I averaged the squared
differences of the observed temperature and the predicted temperature, I got
48.5. This is worse than the
linear function! However, the
equation predicts a temperature of 104.9¡F in 45 minutes, 93.2¡F in 60 minutes, and 72.0¡F in 300 minutes, it is better than linear in the long
term. Why is the error so
large?

This graph shows me that the
equation overestimates the temperature for the majority of the time. So NewtonÕs Law isnÕt perfect, but it
does a pretty good job if you only know 2 data points, and the room temperature.
NewtonÕs Law of Cooling is
often used to estimate the time of death when a body is found. Where else would you use it?