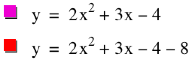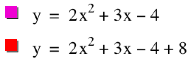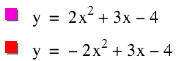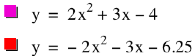Explorations of Second Degree Equations

By: Laura Lowe

Problem:

Graph the parabola y = 2x² + 3x - 4

i. Overlay a new graph replacing each x by (x - 4).

ii. Change the equation to move the vertex of the graph into the second quadrant. 



iii. Change the equation to produce a graph concave down that shares the same vertex.

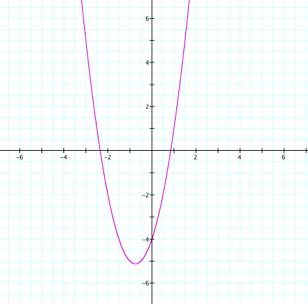
Before graphing y = 2x² + 3x – 4 we can deduce some characteristics from the equation. Since a > 0, we know that the graph is concave up. We also know the y-intercept is (0, -4) because when a parabola is in standard form, as this on is, the y-intercept is (0, c). If we combine these two pieces of information, we can deduce that the function will have 2 x-intercepts. We can also fine the vertex using x = -b/2a and we get (-0.75, -5.125). Now graph the parabola.

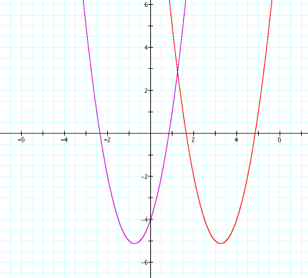
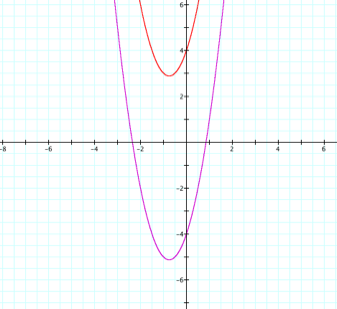
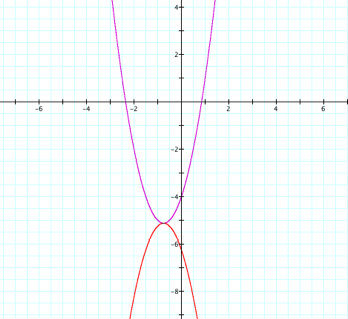
First we are asked to overlay the original graph with a new graph that has each x replaced with (x – 4). We might expect that this would move the graph 4 units to the left.

Replacing each x with (x – 4) has moved the graph 4 units to the right. Why is this? Look at this numerical example.

Let x = 1.

Original function: y = 2(1)² +3(1) – 4 = 1

New function: y = 2(1 – 4)² + 3(4 – 1) – 4 = 2(–3)² +3(–3) – 4 = 5.

So when we subtract 4 from 1, we end up with the same y-value as if we had plugged in –3 in the original function. Let’s look at this on the graph.

So subtracting 4 takes the y-values from four units from the left, thereby moving the function to the right.

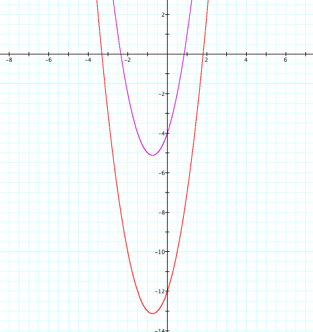
Now, the question asks us to move the vertex of the function to the second quadrant. Since the y-value of the vertex is -5.125, we will have to move the vertex, and with it the entire function, up more than 5.125 units. Let’s move the graph 8 units. My first thought is to try adding 8 to y. This is the same as subtracting 8 from the right side of a function in standard form.

Again, exactly the opposite happened. So, what if we subtract 8 from y? (Add 8 to the right.)

That worked. Why? Try plugging in numbers like we did before and see if you can figure it out.

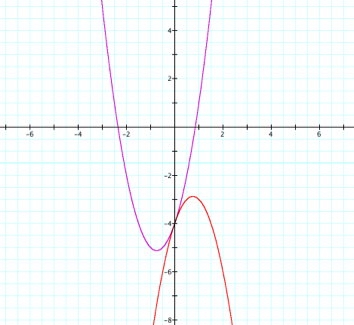
Last we are asked to graph concave down that shares the same vertex. We know for a graph to be concave down a < 0. So we can change y = 2x² + 3x – 4 to y = –2x² + 3x – 4.

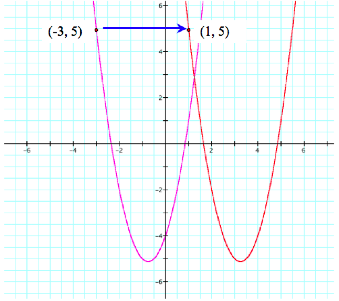
That has changed the function to concave down, but it has also moved our vertex. The new vertex is (0.75, -2.875). So we need to move the function left 1.5 units and down 2.25 units. From what we learned earlier, that means we should add 1.5 to each x and add 2.25 to y. When we expand and simplify we get y = –2x² – 3x – 6.25. Now graph.

That is exactly what we wanted.

Return