Building a Triangle Given the Medians

By: Laura Lowe

Problem: Given line segments j, k, m. If these are the medians of a triangle, construct the triangle.

I began by working backwards to try to find relationships. I started by drawing a triangle and constructing its medians, and then constructed a triangle with sides congruent to the medians of the first triangle. (Click here to see how to construct a triangle from line segments.)

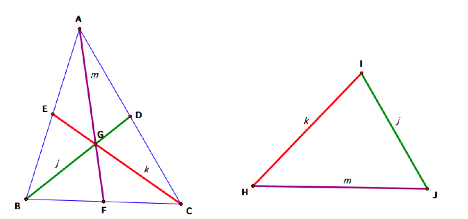
I soon noticed that LEGA LHIJ, LDGA LIHJ, and LDGC LIJH. This means that the angles between the medians of a triangle are the same as the angles between the corresponding sides of the triangle constructed from the medians. So now I knew something about the angles.

I also knew that

and

from the properties of medians.

So now I had enough information to solve the problem: Given line segments j, k, m. If these are the medians of a triangle, construct the triangle.

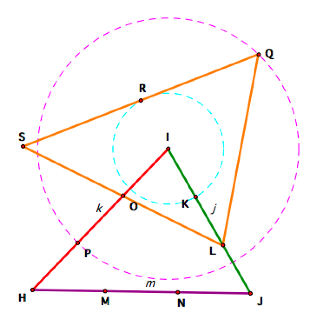
After constructing the triangle from the medians,

I trisected each side.

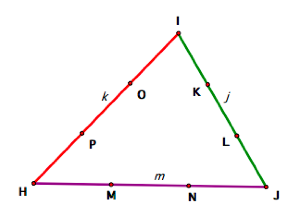
Then I constructed the lines IJ, IH, and a line through I, parallel to HJ.

Now I is the centroid of the triangle with j, k, and m as the medians. (I could have done this for any of the vertices.) Then I constructed a circle with center I and radius IP.

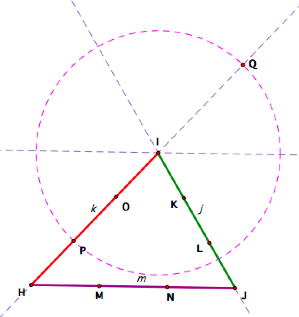
IQ is congruent to k, and is a median of the triangle I am building. Next, I constructed a circle with center I and radius IK.

RL is congruent to j, and is another median of the triangle I am building. This also allows me to construct one side of the triangle, QL. R is also the midpoint of the second side of the triangle, so I constructed the line QR and O is the midpoint of the third side, so I constructed the line LO. The third vertex, S, of the triangle is at the intersection of QR and LO.

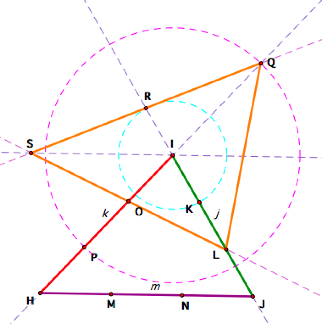
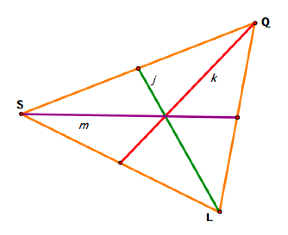
Clean it up a bit and we get:

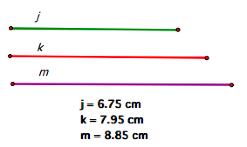
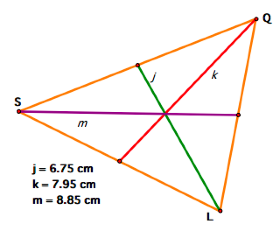
And for those of you who like to see numbers:

Return