Solutions:
1. It
appears that the green figure is an ellipse. (Click here to see my animation.)
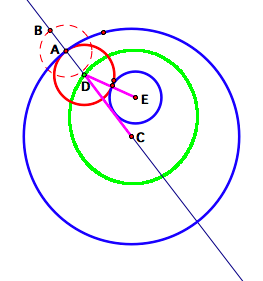
If this is the case, then DC
+ DE would have to be constant. In
fact, DC + DE = BC.
Proof:
Since circles C and E are
fixed, and therefore have a fixed radius, AB and AC are both constant. So BC is constant as well since AB + AC
= BC
BD + DC = BC
DE = BD (from the isosceles
triangle in the construction)
So, DC + DE = BC
2. Again,
it appears that the green figure is an ellipse. (Click here to see
my animation.)
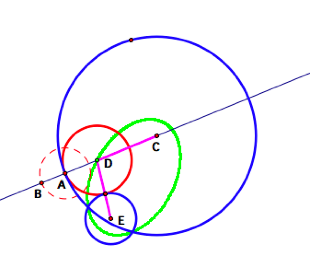
The proof is the same as #1.
3. It
appears that the green figure is a hyperbola. (Click here to see my animation.)
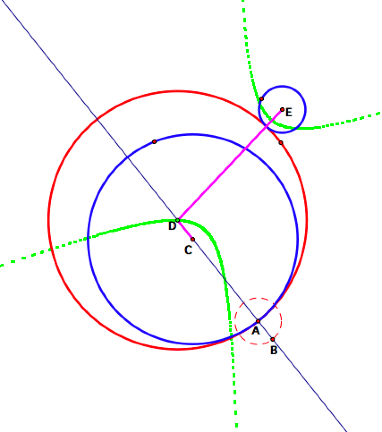
If this is the case, then DC
– DE would have to be constant.
In fact, DC – DE = BC.
Proof:
Since circles C and E are
fixed, and therefore have a fixed radius, AB and AC are both constant. So BC is constant as well since AB + AC
= BC
DE = BD (from the isosceles
triangle in the construction)
DE – DC = BD – DC
BD – DC = –BC
DE – DC = –BC
So, DC – DE = BC