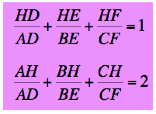Orthocenter Ratios
By: Laura Lowe
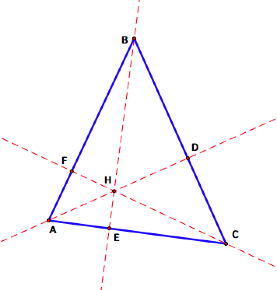
Problem: Given
triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet
of the perpendiculars from A, B, and C respectfully. Prove:
|
|
|
|
Prove:
|
|
Proof:
We can find the area of 
ABC three ways:
since AE is the altitude of
CB, DB is the altitude of AC, and FC is the altitude of AB.
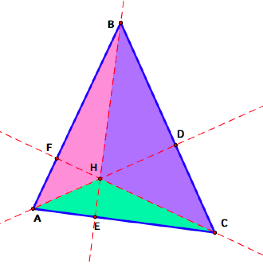
We can also find the areas
of the triangles formed by constructing the perpendiculars.
ABC is divided into 6
smaller triangles by the altitudes BD, AE, and FC. You can also see that 
ABC can be divided onto 3 triangles, 
CHB, 
AHC, and 
BHA. Since BD
AC, and H is on segment BD, HD
AC as well, so we can find the area of 
AHC.
Similarly,
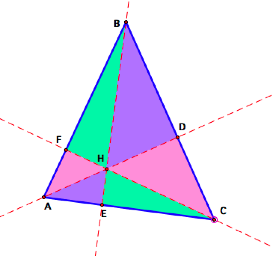
We can express 
ABC = 
CHB + 
AHC + 
BHA. If we
divide both sides of the equation by 
ABC, we get,
We can substitute the
formulas for the areas of 
ABC, 
CHB, 
AHC, and 
BHA that we found earlier and we get:
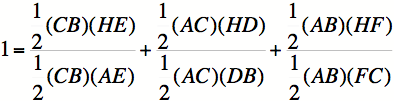
Cancel like terms and we get:
Click here to see my GSP construction with this
calculation.
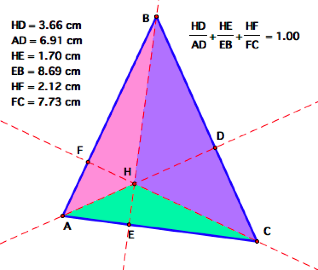
If you manipulate 
ABC so that it is an obtuse triangle, you will see that this
manipulation no longer holds. Why
is this?
|
Prove:
|
|
Proof:
AH = AD – AH
BH = BE – HE
CH = CF – HF
Substitute
into
And
we get
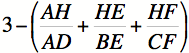
Recall
from the previous proof:
Substitute
and we get:
3 – 1 = 2
Therefore:
Click here to see my GSP construction with this
calculation.
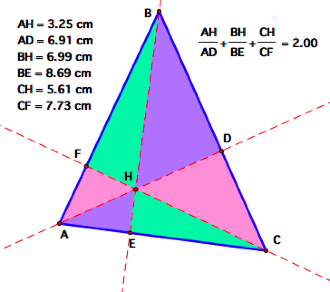
If you manipulate 
ABC so that it is an obtuse triangle, you will see that this
manipulation no longer holds. Why
is this?