Pedal Triangle
By: Laura Lowe
Problem: Let
triangle ABC be any triangle. Then if P is any point in the plane, then the
triangle formed by constructing perpendiculars to the sides of ABC (extended if
necessary) locate three points R, S, and T that are the intersections. Triangle
RST is the Pedal Triangle for Pedal Point P. What if P is the
centroid? incenter? orthocenter? circumcenter? center of the 9 point circle?
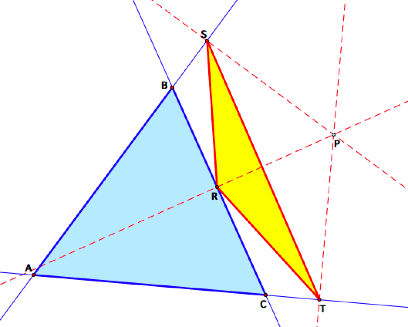
Begin by constructing the pedal triangle for pedal
point P. (Click here
to see my construction.) Use
you construction to manipulate P.
Notice that when P is outside of 
ABC, the pedal triangle RST is sometimes outside of 
ABC,
as above, sometimes a degenerate triangle, and sometimes inside.
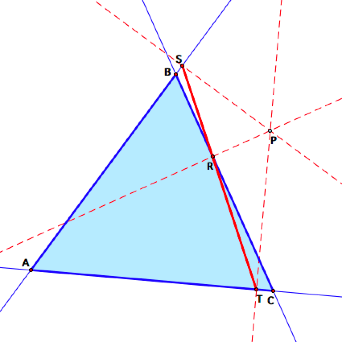
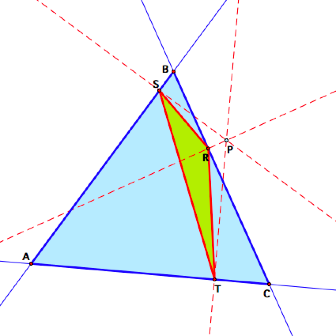
But when P is inside 
ABC,
the pedal triangle is inside as well.
Notice also that when P is
one of the vertices of 
ABC
the pedal triangle is degenerate.
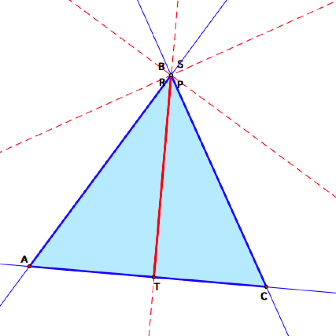
However, these are not the
situations I want to look at today.
LetŐs look at what happens in the 5 cases outlined in the problem
statement.
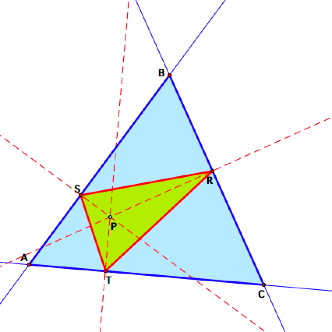
1. The Pedal Point is the centroid of 
ABC.
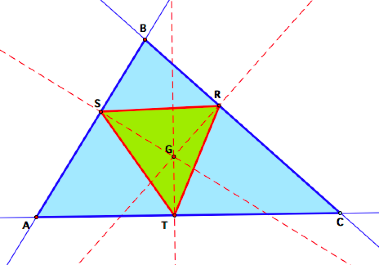
Begin by constructing the
centroid, G, of 
ABC. Then construct the pedal triangle,
using G as the pedal point P.
Remember that the centroid is always in the interior of 
ABC,
so we should expect the pedal triangle to be contained with 
ABC
whether 
ABC
is acute or obtuse. The acute case
is above. Here is the obtuse case.
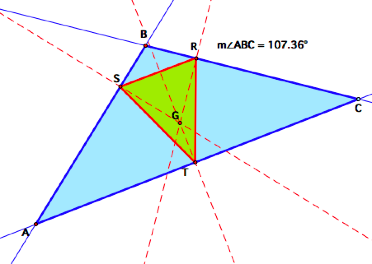
Do you see any other
relationships? Click here to see my construction.
2. The Pedal Point is the incenter of 
ABC.
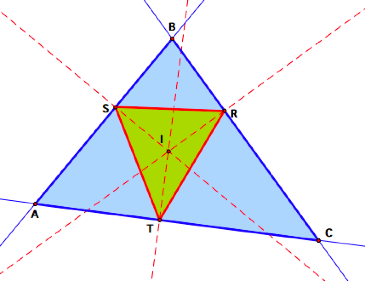
It appears that P is the
circumcenter of 
RST.
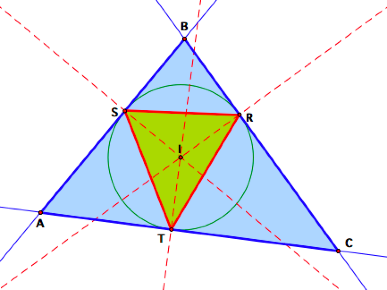
In fact, m(IR) = m(IS) =
m(IT). This is because any point
on the angle bisector is equidistant from the legs of that angle. By definition, point I is on the angle
bisectors of LABC, LBCA, and LCAB.
Do you see any other
relationships? Click here to see my construction.
3. The Pedal Point is the orthocenter of 
ABC.
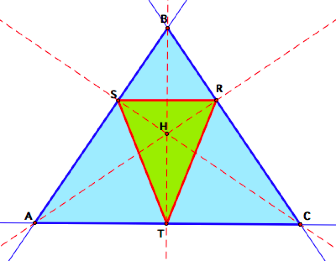
It appears that 
RST is
the orthic triangle of 
ABC. This is because the orthic triangle is
constructed from the altitudes of the triangle. Since altitudes are perpendicular to the sides of 
ABC,
the orthic triangle is a special case of the pedal triangle.
What if
ABC is
obtuse?
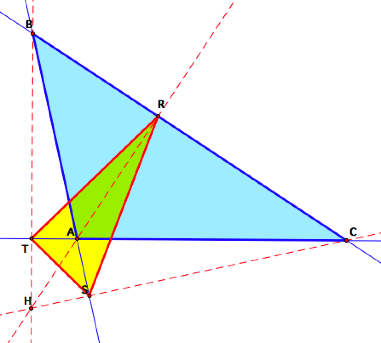
In this case 
RST is
orthic to 
BHC
for the same reason.
Do you see any other
relationships? Click here to
see my construction.
4. The Pedal Point is the circumcenter of 
ABC.
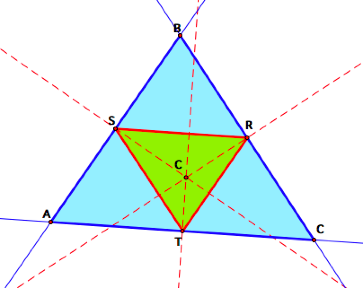
It looks like 
RST is
the medial triangle of 
ABC. This is because the circumcenter is
constructed from the perpendicular bisectors of each side. Therefore m(AT) = m(TC), m(AS) = m(SB),
and m(BR) = m(RC). So point R is
midpoint of side BC, point T is the midpoint of side AC, and point S is the
midpoint of side AB. So 
RST is
the medial triangle. This does not
change when 
ABC is
obtuse.
Do you see any other
relationships? Click here to see my construction.
5. The Pedal Point is the center of the 9
point circle of 
ABC.
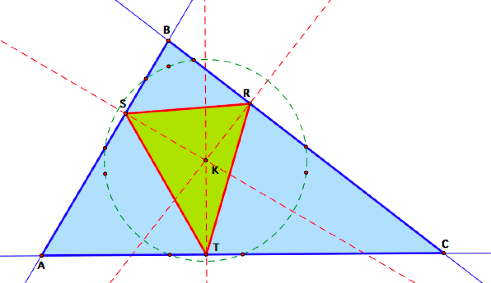
It appears K is on the Euler
Line.
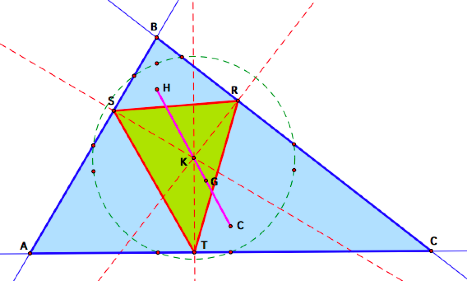
In fact, it looks like K is
the midpoint of the Euler Line.
Why is this?
Do you see any other
relationships? Click here to see my construction.
Some
other interesting constructions:
Click
here to see an animation of the locus
of the midpoints of the sides of the pedal triangle when P is on the incircle.
Click
here to see an animation of the
locus of the midpoints of the sides of the pedal triangle when P is on the
circumcircle.
Click
here to see an animation of the
locus of the midpoints of the sides of the pedal triangle when P is on a circle
larger than the circumcircle.
Click here to see an animation of the locus
of the midpoints of the sides of the pedal triangle when P is on a circle
smaller than the circumcircle.