
Final Project
By: Laura Lowe
Problem 1: Bouncing Barney
Barney is in the
triangular room shown here. He walks from a point on BC parallel to AC. When he
reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and
walks parallel to AB. Prove that Barney will eventually return to his starting
point. How many times will Barney reach a wall before returning to his starting
point? Explore and discuss for various starting points on line BC, including
points exterior to segment BC. Discuss and prove any mathematical conjectures
you find in the situation.
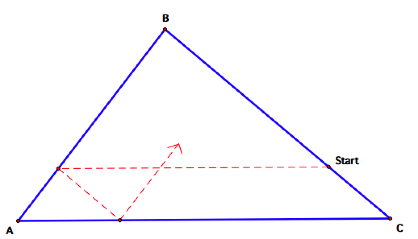
I began by
constructing Barney’s path on Geometer’s
Sketchpad. When I manipulated
Barney’s starting point on segment BC, I found that Barney always returns from
his starting point. He also
appears to take one of two paths.
Either he returns to his starting point after touching each wall twice
(Figure 1), or after touching each wall once. (Figure 2) When he runs into each wall once I will
call that 1 circuit, and when he hits each wall twice I will call that 2
circuits.
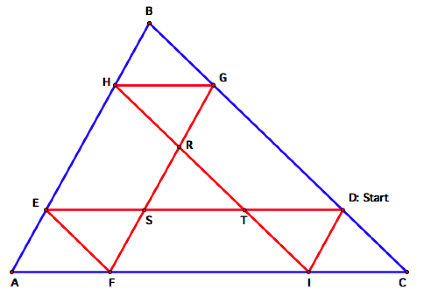
Figure 1
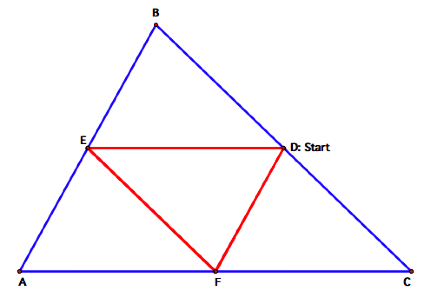
Figure 2
1. It
appears that when Barney only needs 1 circuit to end at his starting point
(Figure 2), it is because he started at the midpoint of segment BC (or at one
of the vertices of rABC).
Proof:
I began by assuming that
Barney starts his journey at the midpoint of segment BC. I know that when a line is parallel to
one side of a triangle and passes through the other two sides, then it divides
the two sides into proportional segments.
Therefore, since Barney started at the midpoint of segment BC, he must
also hit segment AB at its midpoint, E.
By similar reasoning, he must also hit segment AC at its midpoint,
F. And when he leaves the midpoint
of segment AC, he will end at D, the midpoint of segment BC, his starting
point. Q.E.D.
It
falls from this proof that Barney’s path is the medial triangle of rABC since he hits the midpoint of each side. I also
know that when a midsegment (the segment between the midpoints of two sides of
a triangle) is parallel to the third side of the triangle, its measure is half
the measure of the third side.
This means
DE = ½AC, EF = ½BC, and FD = ½AB
DE + EF + FD = ½(AC + BC + AB)
So Barney’s path is half the
length of the perimeter of rABC.
2. If
Barney starts anywhere other than the midpoint or one of the vertices of side
BC of rABC, he needs two circuits to return to his starting
point (Figure 1).
Proof:
Suppose Barney does not meet
return to his starting point and instead ends his two circuits at a point J on
segment BC. (Figure 3)
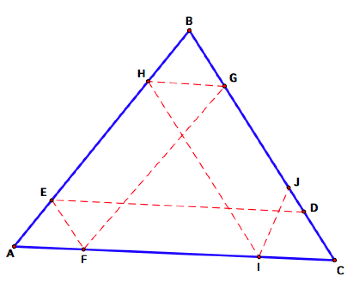
Figure 3
Let Barney start his path at a point D on side BC. He then runs into segment AB at a point
E. Since when a line is parallel
to one side of a triangle and passes through the other two sides it divides the
two sides into proportional segments, I know that
![]()
By
the same reasoning, when Barney runs into segment AC at point F, I know that
![]()
Similarly,
![]()
![]()
![]()
![]()
So
by transitivity,
![]()
Therefore BD = BJ. Which is a contradiction. So D and J are the same point, and
Barney returns to his starting point in 2 circuits. Q.E.D.
Conjecture: The length of Barney’s path equals the
perimeter of rABC, when he starts anywhere other than the midpoint
or one of the vertices of side BC of rABC.
Proof:
LEBD ![]() LFGC by corresponding angles
LFGC by corresponding angles
LBDE ![]() LGCF by corresponding angles
LGCF by corresponding angles
m(BD) ![]() m(GC)
m(GC)
Therefore, rBED ![]() rGFC by Angle, Side, Angle
rGFC by Angle, Side, Angle
and m(ED) = m(FC)
LBHG ![]() LAEF by corresponding angles
LAEF by corresponding angles
LAEF ![]() LHBG by corresponding angles
LHBG by corresponding angles
m(AE) = m(HB)
Therefore, rAEF ![]() rHBG by Angle, Side, Angle
rHBG by Angle, Side, Angle
and m(HG) = m(AF)
Since m(ED) = m(FC) and m(HG)
= m(AF),
m(AF) + m(FC) = m(HG) + m(ED)
m(AC) = m(HG) + m(ED)
Similarly,
m(AB) = m(FG) + m(ID)
m(BC) = m(HI) + m(EF)
Therefore
m(AB) + m(BC) + m(AC) = m(FG)
+ m(ID)+ m(HI) + m(EF) + m(HG) + m(ED) Q.E.D.
3. What
if Barney starts on a point outside of rABC? (Figure 4)
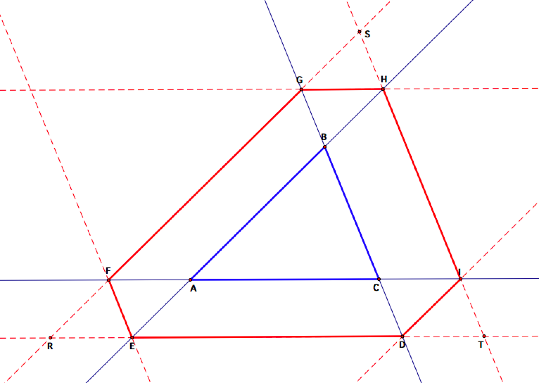
Figure 4
It appears that he will still
return to his starting point.
Proof:
Since RS || AB and ST || BC, LRST ![]() LABC
LABC
Since ST || BC and RT || AC, LSTR ![]() LBCA
LBCA
Since RT || AC and RS || AB, LSRT ![]() LBAC
LBAC
So, rABC and rRST are
similar. And since D, E, F, G, H,
and I are on rRST, Barney
will always return to his starting point. Q.E.D.
Return
to Final Project
Return to my
Home Page