Let's begin by looking at the parametric equations which will give us a simple circle--radius 1 and center (0,0)

Now, let's suppose we want to change our circle. Say, we want a circle with radius 4. How can we change our equations so that our graph will become a circle with center (0,0) and radius 4?

(Based on previous graphing experience, I would hope that the class would suggest multiplying and then we could explore what happens when we multiply the t by a constant and what happens when we multiply the trig function by a constant. Initially, I would consider the case where a = b with the students.)

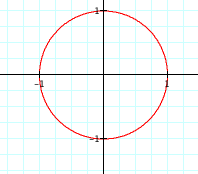
A good starting point might be to let both a and b = 4. When we do, our graph looks like this:

Why is our graph unchanged by multiplying t by 4 in each equation?

(Hopefully, this question will lead to a discussion of the fact that multiplying t by 4 in each equation just takes around the circle "faster")

Since multiplying t by a constant didn't work, let's try giving the trig functions a coefficient?

What happens if multiply each of the trig functions by 4? a = b = 4

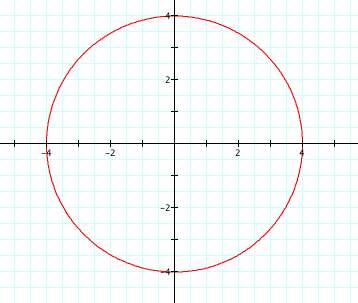
Why did multiplying the trig functions by 4 work?

(Hopefully this question will lead to a discussion of how this "stretches" the graph. I will eventually focus on the point where we cross the axes and see that what we multiply cos t by gives us the points where we cross the x-axis and what we multiply sin t by gives us the points where we cross the y-axis.)

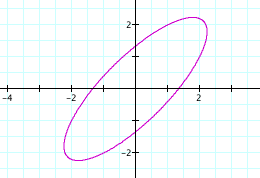
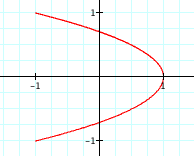
What do you think will happen if a does not equal b? Will we still get a circle? If not, what shape will our graph have?

(In class, I would let the students generate values of a and b to explore, being sure that we had examples of both a<b and a>b. But, for this write-up, lets look at a = 3 and b = 5)

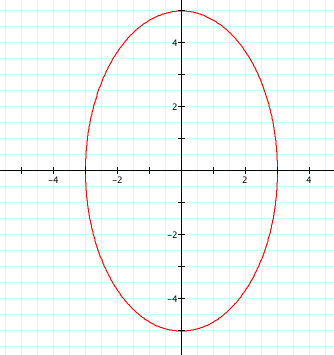
Why do we now have an ellipse instead of a circle now?

(Hopefully, this will lead to a discussion of the fact that we are now "stretching" the graph differently in the horizontal and vertical directions. After many examples, I would like for students to conclude that if a > b, the major axis of the ellipse will be horizontal and that if b > a, the major axis will be vertical. I would also like for them to notice that we have not yet changed the "center" of the figure. That in each case, the major and minor axis intersect at (0,0).)

So, now we have figured out how to alter our graph to create a circle with a particular radius and how to create ellipses with axes of certain lengths. When we looked at the equations below where a and b were equal we just got our original circle. Do you think this will still be the case if a and b are not equal?

(Below are some of the a and b values I might try with students--I would let them come up with values and would expect that their initial choices would be integers. First, I would like the discussion to focus on WHY we no longer have a circle. Then, I would like for them to find some patterns of what the graph will look like based on the values of a and b--for example when a=1, how does the value of b relate to the number of "pieces" of our graph and vice versa.)

a = 3; b = 4

a=1; b=2

a = 1; b = 3

a = 1; b = 4

a=2; b=1

a = 3; b = 1

a = 4; b = 1

a = 5; b = 1

What if we choose a value that is not an integer, how does that impact the patterns we have been seeing?

a = 1; b = 1.75

a = 1; b = 2.3

a = 1; b = 3.7

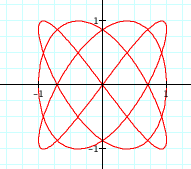
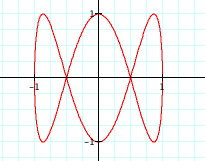
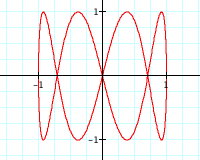
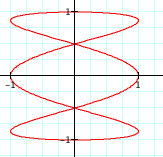
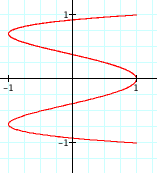
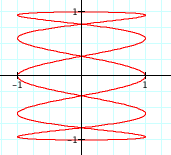
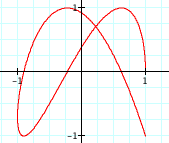
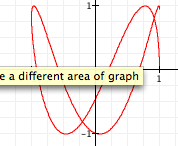
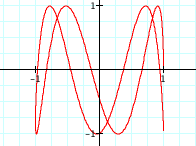
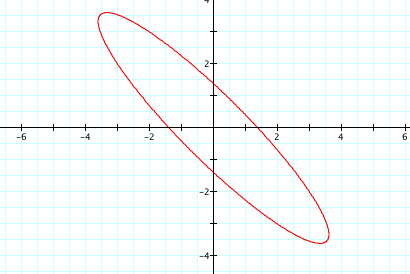
Finally, let's explore the following parametric equations:

How do these equations relate to the equations we were just exploring?

(Hopefully, they will notice that if h = 0, we have the equations we were just working with!)

How do you think the changes to the equations will affect the graph?

(I would expect them to suspect some type of translation because of the addition. I attempt to begin examples where we do not have a = b = h or even a = b. I would like them to first make a connection between h and the slope of the major axis of an ellipse. We would look at several examples, but one is below)

What do you think will happen if a = b? Do you think we will have a circle?

(I would expect them to guess that this is a circle. I would like to start with h not equal to a and b, so that we continue to get an ellipse and to explore why we have an ellipse and not a circle. below is one possible example, a = b = 3 and h = -2)

Now, what if a = b = h? What will you expect the graph to look like?

(I think they might again guess that this would be a circle. I would not expect them to predict that it is a line based on the graphs we have looked at so far. I would then direct them back to the actual equations to figure why we are getting a line and would hope that someone would conclude that it is actually the line y = x because for all values of t, when a = b = h, x and y are equal).