This
lesson is influenced by the Mathematics in Context curriculum for middle
school students, but could be used for College Algebra students as well.
You would need to allow different amounts of time for different age groups.
Divide the students
into small groups (approximately four people). Begin by handing out a
rectangular sheet of papers (all the same size), tape, and scissors. Ask
them to work in their groups to figure out how to make a lidless box and
then for each student in the group to make a box. Hopefully, students
will realize that they must cut squares out of each corner and fold up
the sides to get a box.
Once multiple boxes
(hopefully not all with the same dimensions) have been created, we can
begin to talk about the size of the box. The discussion could be initiated
by asking the students who has the "biggest" box and once they
have made a choice to explain why that box is the biggest. Hopefully,
different students would give different answers and explanations. Some
possible choices would be the box with the largest height, the box with
the largest width, and the box with the largest volume (perhaps described
as the box that could hold the most stuff).
After a discussion
of the different ways of looking at the size of the box, I would focus
the class on the box's volume. After looking at maximizing volume we could
look surface area and address issues related to height and width. I would
now give each group tools to measure the volume of the boxes (rulers and
cubes come to mind) and ask the groups to determine the volume of each
box. After this task was completed we could discuss the different methods
used to determine the volume of the box. Hopefully, this discussion will
lead to the possibility of using the formula V = lwh.
At this point we
will have some data to explore. I would make a table displaying the size
of each student's box. A sample is below based on initial paper size of
5 x 8.
|
Student Name |
Volume of Box
(in cubic inches)
|
| Emily |
8 |
| Vance |
15 |
| Keesha |
8.4375 |
| Griffin |
14 |
| Will |
18 |
| Maddie |
8 |
| Jack |
8.5 |
Now, we would need
to address why we are getting different size boxes if
that has not already been determined. The goal of this discussion would
be to see that the length of the side of the square we cut off becomes
the height of the box and determines the length and the width. We could
create a table with the dimensions of each students' box. A sample is
below.
| Student Name |
height (in inches) |
length (cut from 8 in side) |
width (cut from 5 in side) |
| Emily |
2 |
4 |
1 |
| Vance |
1.5 |
5 |
2 |
| Keesha |
.25 |
7.5 |
4.5 |
| Griffin |
.5 |
7 |
4 |
| Will |
1 |
6 |
3 |
| Maddie |
2 |
4 |
1 |
| Jack |
.25 |
7.5 |
4.5 |
From this data, we could determine
that l = 8 - 2h and w = 5 - 2h.
Now, I would ask if they think
we have created all possible boxes. Hopefully, through this discussion
the students would determine that we had not and since we had not created
all possible boxes, we could not know for sure that Will's box has the
largest possible volume. And now, finally, we have motivation to use technology
to help us. Technology can allow us to simulate making many more boxes.
The type of discussion used
to introduce excel would depend on the amount of experience the students
had with excel. Our first discussion with regards to excel would be how
to choose the values of h--the length of the side of our box. If possible
I would like for each group to work in excel and come up with a list of
possible values for h, l, w, and V. Then come back together as a large
group and discuss the problems we encountered and how we determined the
possible values for each variable. This discussion would hopefully lead
to an understanding of the constraints of the problem.
Hopefully at least one group
would include 0 as a possible value for h and we could discuss why 0 gives
us a volume of 0. Or, if no group includes 0, maybe at least one group
will have consciously excluded it because it does not result in a box
being made.
It is more likely that groups
will, at least initially, choose values of h that equal and exceed 2.5
and we can discuss why h must be less than 2.5. We could even allow them
to go back to their paper and scissors and see what happens when we cut
off a square with side lenght 2.5 inches.
Below are some possible tables
the students might come up with and some possible points of discussion:
Choose only integer values
for h: discuss why this might not be sufficient--discuss meaning of negative
values
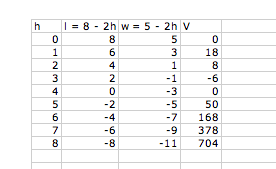
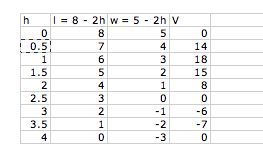
Choose h = 0 as start and increase
by .5: Is this enough values to try? Where should our table stop?
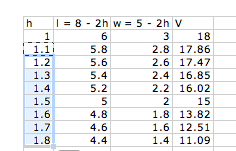
Choose h = 1 as start and increase
by .1: Is it okay to start with 1? Why is 0 not on the list? What other
values could we choose to start with? Do you have enough values?
My ideal chart for
this question:
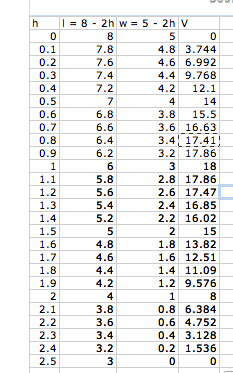
What we have done
so far could be done with many levels of students. Depending on the level
of the students, I would next go into defining the volume of the box as
a function of the height V = h(8 - 2h)(5-2h) and graph it:
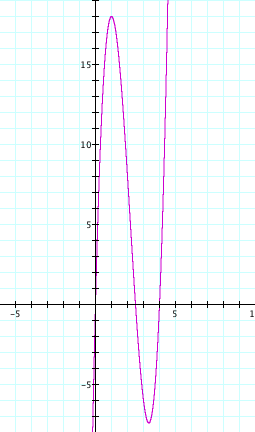
We can now discuss
that h is our dependent variable and V is our independent variable and
that we often use x and f(x) or y to play these roles. We can also discuss
how the graph relates to the data we collected. In small groups, I would
ask the students to come up with an interpretation of the graph to share
with the larger group. In particular, I would try to focus them in on
which part of the graph represents our data and why the rest of the graph
is not of interest to us in this case. This could lead to a discussion
of domain and why we sometimes restrict the domain of a graph and how
restricting the domain may result in restricting the range.
Finally, I would
ask them if they are convinced that the box with the maximum volume is
created when h = 1? I would expect them to be convinced at this point.
Then I would ask them if we have proven that this is
the case. This question would hopefully lead to some discussion and would
create a desire to know how to prove what seems so obvious at this point.
Depending on the
level of the students, I might at this point introduce the concept of
the tangent line and its slope--not at the level of determining the derivative,
but more as a way to motivate interest in calculus. Sometimes students
seem to see Calculus as this separate subject that lies ahead of them.
I think it is nice to introduce Calculus concepts early on so it does
not seem as intimidating of a subject.
Alternately or
in addition, we could go back to quadratic equations and identifying the
max or min of those functions algebraically.
|





