Let's explore the roots of the following equation:

ax^3 + bx^2 + cx + d = 0

Before we begin looking at graphs, consider the following questions:

• How many roots will this equation have?
• What kinds of roots (real, imaginary, complex) can this equation have?

Now, we will begin exploring how the values of each of the coefficients a, b, c, and d relate to the roots of the equation. We can do this by looking at the graphs in each of the following planes:

• The xb plane
• The xc plane
• The xd plane
• The xa plane

How can we explore the equations in these planes using graphing calculator?
(Just curious to see if the class can come up with the idea of replacing the coefficient with y before I introduce the idea.)

Below is a graph of ax^3 + bx^2 + y x + d = 0; (a = 1, b=1, and c=1)

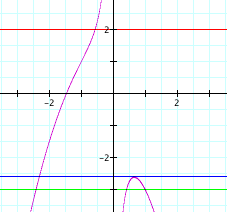
The red line represents y=2. Describe the roots of the equation when y = 2. How many roots are represented by this graph when y=2? Are there roots of the equation not represented by this graph when y=2?

The green line represents y = -3. Revisit the above questions when y=-3

How would you interpret the blue line on the graph?

Below is a graph of ax^3 + yx^2 + cx + d = 0; (a = 1, c=1, and d=1)

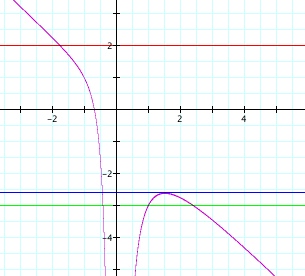
The red line represents y=2. Describe the roots of the equation when y = 2. How many roots are represented by this graph when y=2? Are there roots of the equation not represented by this graph when y=2?

The green line represents y = -3. Revisit the above questions when y=-3

How would you interpret the blue line on the graph?

Below is a graph of ax^3 + bx^2 + cx + y = 0; (a = 1, b=1, and c=1)

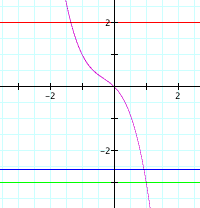
In this graph no matter what the value of y, y =d only crosses the graph once--How do you interpret this fact?

What should we do to explore this situation more?
(Hopefully, a student will suggest changing the values of a, b, and c.)

Below is a graph of ax^3 + yx^2 + cx + d = 0; (a = -1, c=2, and d=3)

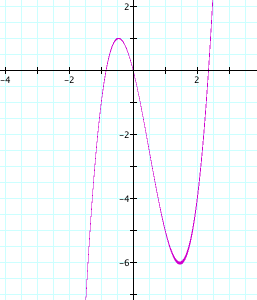
For what values of d does the equation -x^3 +2x^2 + 3x + d = 0 have three real roots?

Can this equation--or any third degree equation with integer coefficients--ever have exactly two real roots? Explain why or why not.

(This question should lead to the idea of one of the roots being a "double" root--and that is the only case where this can happen. In particular, I want them to see that one complex root and two real roots won't lead to an equation with integer coefficients)

Below is a graph of yx^3 + bx^2 + cx + d = 0;

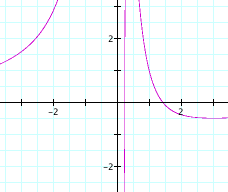
It appears that when y = .5, that the equation has exactly two distinct real roots--is this possible?

How can we explain the way this graph appears? How many times do you think the line y = .5 actually intersects this graph?