This write-up explains given the picture below how to construct a point X on segment AC and a point Y on segment BC such that the lengths of AX, XY, and YB are equal.

To begin the construction we will pick a random point X' on the segment AC and use this point to construct segments AC' and C'B' and point Y' such that the lengths of segments AX', X'Y', and Y'B' are equal. We can then project point Y' onto segment CB to find point Y and use point Y to construct point X on AC.

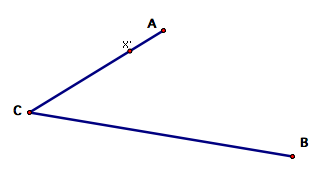
To reiterate, we begin by constructing point X' on segment AC.

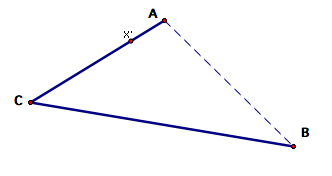
Next, we construct segment AB.

Construct a circle with center X' and through the point A.

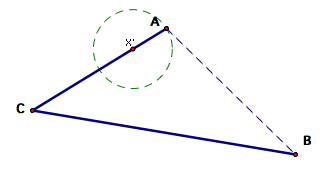
Construct a line through X' and parallel to segment CB.

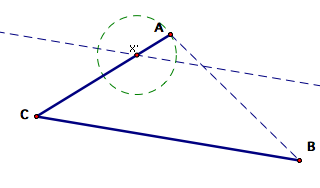
Find the intersection of the newly constructed line and the circle X'.

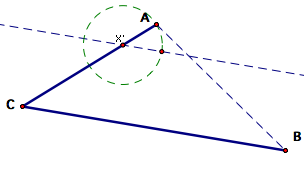
Construct a circle with center the intersection of the line and circle and through point X'.

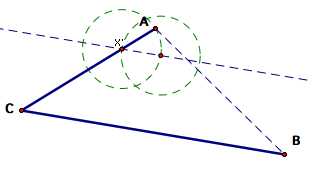
Find the intersection of the newly constructed circle and the segment AB.

Construct a line through this intersection and parallel to the line segment CB.

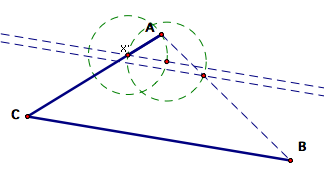
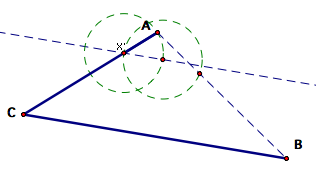
Find the intersection of the new line and the original circle. Note that there are two intersections but in this case we want the intersection on the right side of the circle. This choice will be of particular interest later in the write-up.

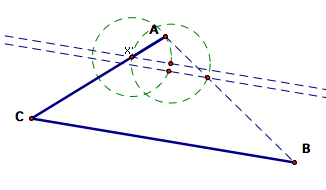
Connecting these four points we create a rhombus. Note that if we had chosen the other intersection in the previous step, we would not have a rhombus. We know that this is a rhombus because three sides are radii of the two circles and the circles were constructed to have the same radius and one pair of sides is parallel by construction. This means the fourth side must be of the same length and parallel to the side opposite it.

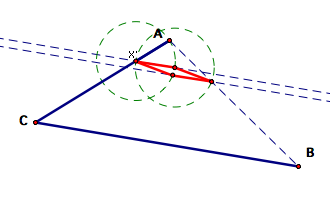
In addition, we have now created our C', B', and Y' such that the lengths of AX', X'Y', and Y'B' are equal (they are each the radius of one of the circles and the circles were constructed to have the same radius).

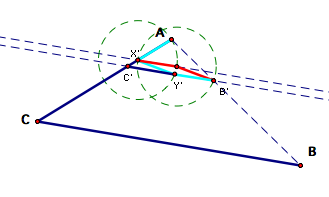
We will now construct a line through A and Y'. Where this line intersects CB will be the point Y.

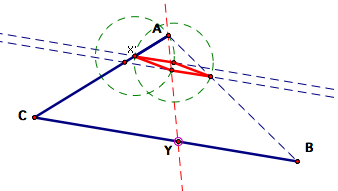
Because we want to construct a similar figure, we will construct a line through the point Y and parallel to the line X'Y'.

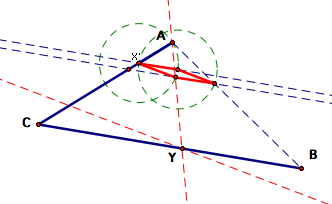
Where this line intersects the segment CA is the point X. Measuring the segments XA, XY, and YB shows that we have succeeded in constructing the desired points X and Y in this particular case.

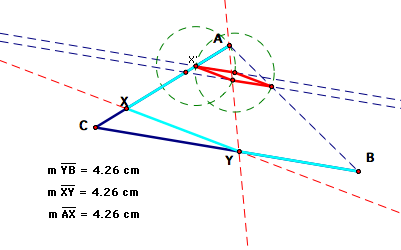
By constructing a line through X and parallel to CB, and a line through B and parallel to XY, we can find the rhombus in this situation.

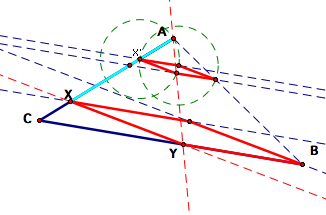
We can verify that this structure is a rhombus by constructing centered at Y and B and both with radius XY.

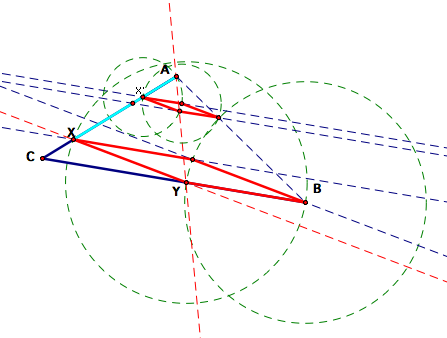
We have successfully completed the construction of points X and Y in this situation, but we would like to know that this construction will work in all situations. Unfortunately, it does not. If we drag A far enough to the right, the segments AX, XY, and YB are no longer of equal length--as shown below.

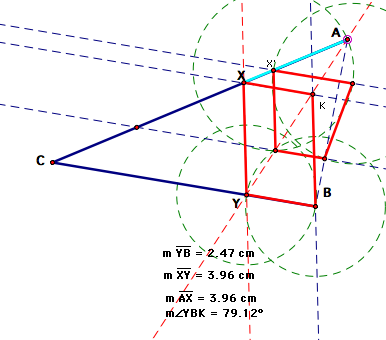
It appears that the current construction does not work once A moves to the right of B--or that it works as we move A to the right up until the point the rhombus becomes a square.

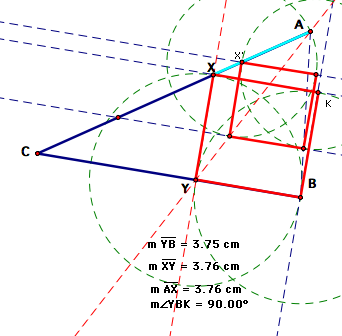
To explore this situation further, I began the construction again, but this time began with a picture where A was to the right of B. In this situation, when we reach the point of choosing the intersection of circle F (below) and the line through points E and G, we choose the intersection on the left to create our rhombus. In the previous construction, we chose the intersection on the right.

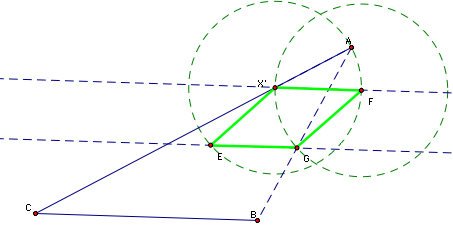
This procedure again allows us to identify Y' (E below).

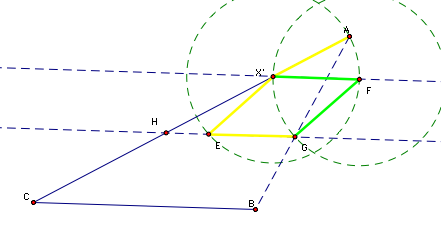
And use the line through A and Y' (E below) to locate Y. This time, I used a circle centered at Y through B to locate X. This technique also allowed me to correctly identify the desired X and Y in this situation as verified by the measurements below.

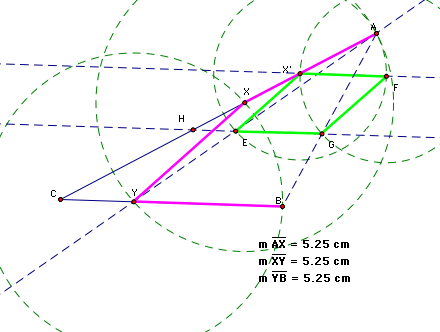
Using this construction, when A moves to the left of B, the segments AX, XY, and YB are no longer of equal length and our figure is no longer a rhombus.

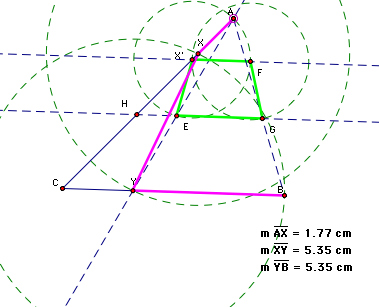
It seems that which intersection forms a rhombus changes depending on whether A is to the left or right of B initially. If A is directly above B, we will have a square, the circle will be tangent to the line and we will only have one point of intersection.