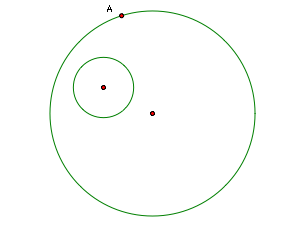
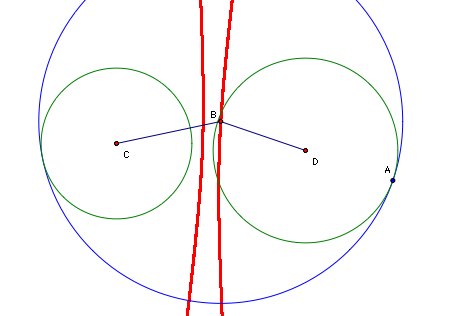
Given a circle within a circle and a point A on the outer circle, as seen below, we can construct a circle tangent to the outer circle at point A and tangent to the inner circle.

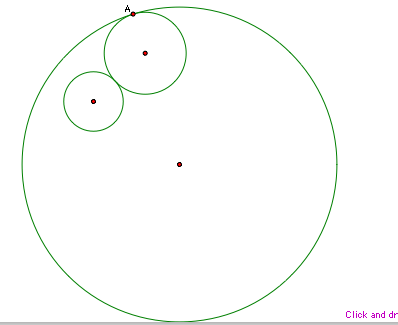
We can create the tangent circle, so that the original smaller circle is outside the tangent circle. Clicking the image below will open the tangent circle tool in GSP.

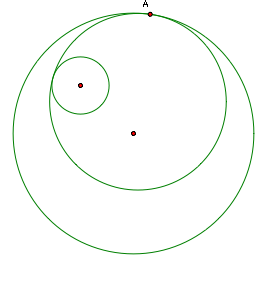
We can also create the tangent circle so that it envelops the smaller original circle. Clicking on the image below will bring up this tangent circle tool in GSP.

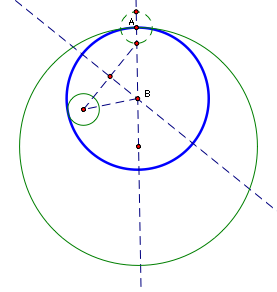
The constructions for each of the two tangent circles are very similar. We begin by creating a line through the center of the larger circle and point A.

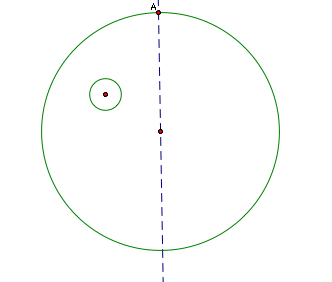
Next we construct a circle with center point A and radius of equal length to the radius of the inner circle.

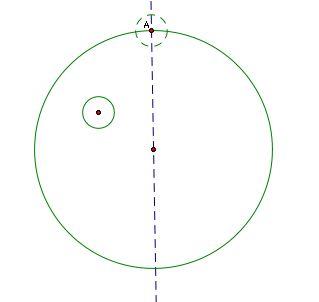
This new circle with center point A will intersect the constructed line in two locations--one inside the larger circle and one outside the larger circle.

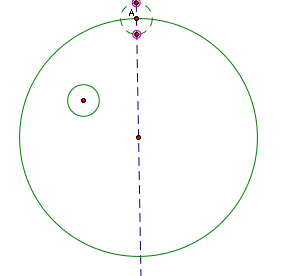
We will construct a segment from the center of the smaller circle to one of the points of intersection just constructed. This choice will lead to the two possible tangent circles. If we choose the point outside the circle, the result will be the tangent line that does not contain the smaller circle. If we choose the point of intersection inside the larger circle, the result will be the tangent circle that envelops the smaller circle.

In either case, we will then construct the perpendicular bisector of this segment.

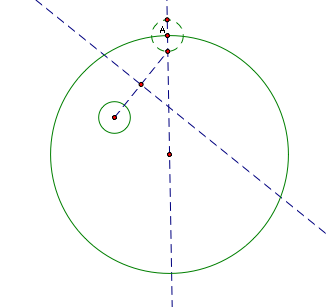
Using the point where the perpendicular bisector intersects the existing line, we can create an isosceles triangle.

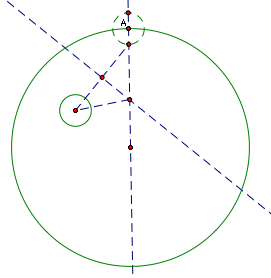
Now, a circle with center point B and passing through point A will be tangent to both existing circles. (The distance from B to A is the length of the side of the isosceles triangle plus the radius--if we look at the distance from B through the center of the smaller circle to the other side of the circle, it is the same.)

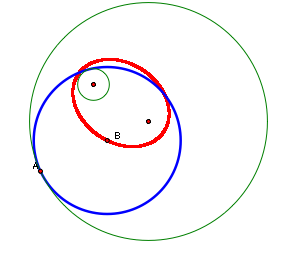
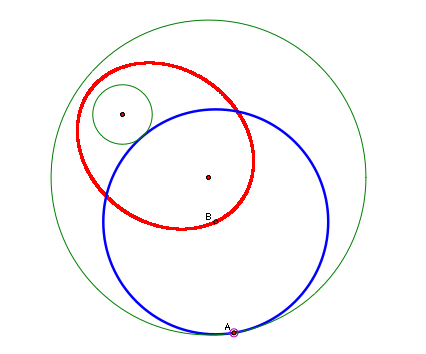
Now let's explore the locus of point B as point A moves around the circle. What shape will it have?

In both cases, the locus appears to be an ellipse with the foci being the two centers of our original circles.

To verify that the locus is an ellipse with foci being the two centers of our original circles, we must show that the sum of the distances from B to each center is constant. Click here to see a GSP animation of the sums of the distances.

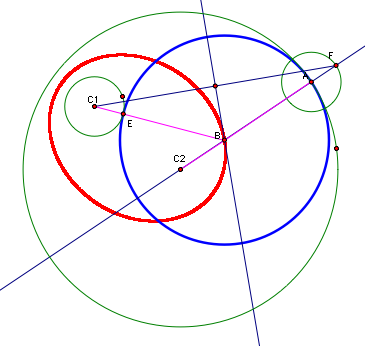
We can also prove the sum of these distances is constant geometrically. In the picture below, the length of segment C2F is constant because segment C2A is a radius of a fixed circle and segment AF is the radius of a fixed circle. The length of segment EB always equals the length of segment BA because they are radii of the same circle. The length of segment C1E is equal to the length of segment AF by construction. The length of C2B is also always equal to itself. These equivalencies give us that the length of segment C1E + the length of segment EB + the length of segment BC2 EQUALS the length of segment AF + the length of segment BA + BC2. Which simplifies to length of segment C1B + the length of segment BC2 = the length of segment C2F. Since C2F is a constant, the sum of the lengths of segments C1B and BC2 is constant.

What happens if rather than having the smaller circle contained in the larger circle, we allow the circles to intersect?

In this situation, the two cases appear to yield different results. When we look at the tangent circle that does not envelop the smaller circle, we appear to get an ellipse again. Click here to see an animation of point A and a calculation of the ellipse distances.

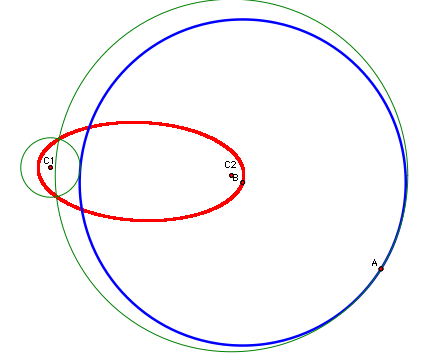
Again, we can prove that the figure is an ellipse geometrically. In the picture below, the length of segment C2E is constant because segment C2A is a radius of a fixed circle and segment AE is the radius of a fixed circle. The length of segment FB always equals the length of segment BA because they are radii of the same circle. The length of segment C1F is equal to the length of segment AE by construction. The length of C2B is also always equal to itself. These equivalencies give us that the length of segment C1F + the length of segment FB + the length of segment BC2 EQUALS the length of segment AE + the length of segment BA + BC2. Which simplifies to length of segment C1B + the length of segment BC2 = the length of segment C2E. Since C2E is a constant, the sum of the lengths of segments C1B and BC2 is constant.

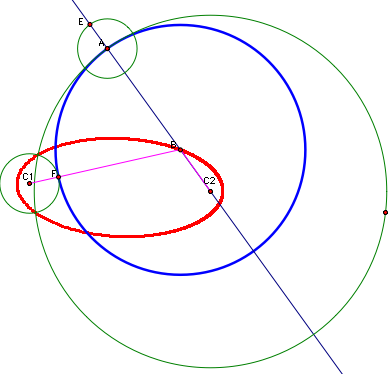
In contrast, when we look at the case where the tangent circle does envelop the smaller circle, we appear to get a hyperbola. Click here to see an animation of point A and a calculation of the hyperbola distances.

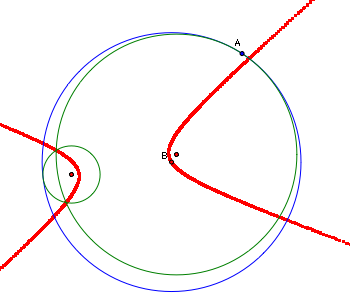
We can also prove that locus is a hyperbola geometrically. In the picture below, we want to show that the length of segment CB - the length of segment BD is a constant. To begin with, let us note that the length of segment FD is constant because it the difference of two constants. The length of segment AD is constant because it is the radius of a fixed circle. The length of segment AF is constant because it is the radius of a fixed circle. And, the length of AD minus the length of AF equals the length of FD.

Now, we can show that the length of segment CB minus the length of segment BD equals the length of segment FD.

the length of FD = the length of AB - the length of AF - the length of DB.

Substitute the length of BH for the length of AB as they are radii of the same circle. Substitute the length of HC for the length of AF as they are the same by construction.

the length of FD = the length of BH - the length of HC - the length of DB

But BH - HC is BC, so we can substitute again.

the length of FD = the length of BC - the length of DB

Finally, let us look at what happens with the two original circles are do not intersect and one is not contained within the other. In this situation, the locus of B appears to be a hyperbola regardless of which case we look at. Click either image to see the associated animations and calculations.

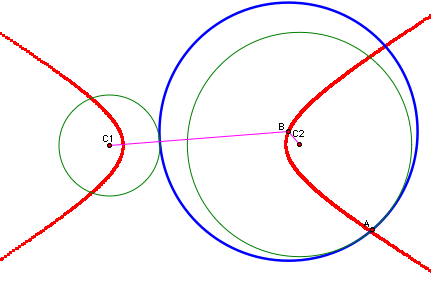
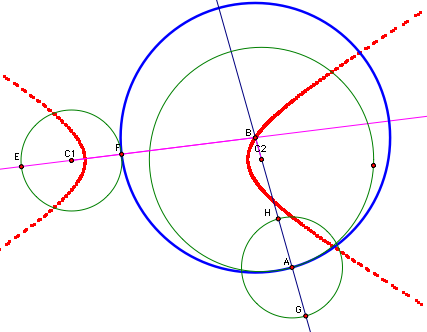
Again, we can prove this geometrically. In the picture below, we want to show that the length of C1B minus the length of segment BC2 is constant.

The length of segment C2G is constant because it is the sum of the length of segment C2A (radius of a fixed circle) and the length of segment AG (radius of a fixed circle).

Also, the length of segment C2G = the length of segment BG - the length of segment BC2

The length of segment BC1 = the length of BG, so we can substitute.

the length of segment C2G = the length of segment BC1 - the length of segment BC2