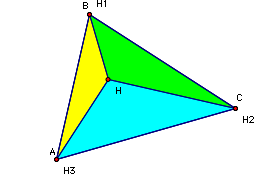
Orthocenters and the Nine Point Circle
by Margaret Morgan
- The midpoint of each side of the triangle (3 points)
- The foot of each altitude (3 points)
- The midpoints of the segments from the vertex to the orthocenter (3 points)
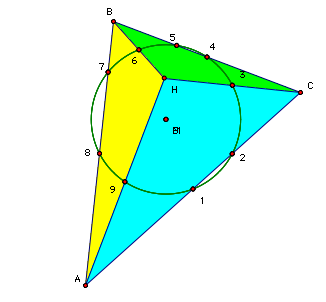
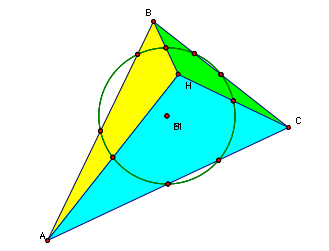
The above is constructed to be the nine point circle for the triangle ABC. By construction the following follow:
- Point 1 is the midpoint of segment AC
- Point 4 is the midpoint of segment BC
- Point 8 is the midpoint of segment AB
- Point 7 is the foot of the altitude from C to segment AB
- Point 5 is the foot of the altitude from A to segment BC
- Point 2 is the foot of the altitude from B to segment AC
- Point 3 is the midpoint of segment HC
- Point 6 is the midpoint of segment HB
- Point 9 is the midpoing of segment HA
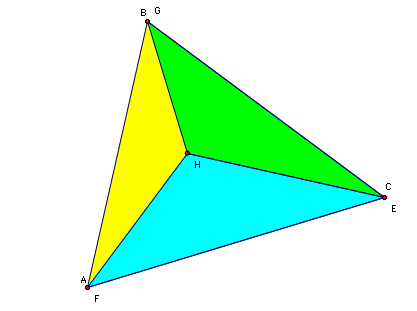
Let us show this circle is also the nine point circle for triangle HAC
- The circle passes through the midpoint of each side of the triangle (Point 1 is the midpoint of AC, Point 3 is the midpoint of HC, and Point 9 is the midpoint of HA)
- The point B is the orthocenter of triangle HAC (see proof below); The circle passes through midpoint of the segment from the orthocenter (B) to each of the vertices (Point 6 is the midpoint of HB; Point 4 is the midpoint of BC, Point 8 is the midpoint of BA)
- The circle passes through foot of each altitude. (Point 2 is the foot of the altitude from H--the segment from B to point is the altitude and H lies on this segment by construction, Point 7 is the foot of the altitude from vertex A--segment C7 is perpendicular to AB, Point 5 is the foot of the altitude from C--by construction A5 is perpendicular to BC.)
Let us show this circle is also the nine point circle for triangle HBC
- The circle passes through the midpoint of each side of the triangle (Point 6 is the midpoint of HB, Point 3 is the midpoint of HC, and Point 4 is the midpoint of BC)
- The point A is the orthocenter of triangle HBC (see proof below); The circle passes through midpoint of the segment from the orthocenter (B) to each of the vertices (Point 9 is the midpoint of HA; Point 1 is the midpoint of AC, Point 8 is the midpoint of BA)
- The circle passes through foot of each altitude. (Point 5 is the foot of the altitude from H--the segment from A to point 5 is the altitude and H lies on this segment by construction, Point 7 is the foot of the altitude from vertex B--segment C7 is perpendicular to AB, Point 2 is the foot of the altitude from C--by construction B2 is perpendicular to AC.)
- The circle passes through the midpoint of each side of the triangle (Point 6 is the midpoint of HB, Point 9 is the midpoint of HA, and Point 8 is the midpoint of BA)
- The point C is the orthocenter of triangle HAB (see proof below); The circle passes through midpoint of the segment from the orthocenter (B) to each of the vertices (Point 4 is the midpoint of CB; Point 3 is the midpoint of HC, Point 1 is the midpoint of AC)
- The circle passes through foot of each altitude. (Point 7 is the foot of the altitude from H--the segment from C to point 7 is the altitude and H lies on this segment by construction, Point 2 is the foot of the altitude from vertex A--segment B2 is perpendicular to AC, Point 5 is the foot of the altitude from A--by construction A5 is perpendicular to BC.