Return to Class Page

Pedal Triangles and the Simson Line

by Margaret Morgan

Let us briefly review how to construct a pedal triangle given a triangle and a point P.

Begin by extending the segments AB, BC, and AC to become lines.

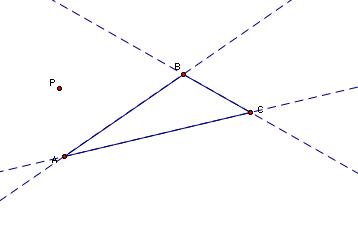
Then construct lines through P and perpendicular to each of the three lines.

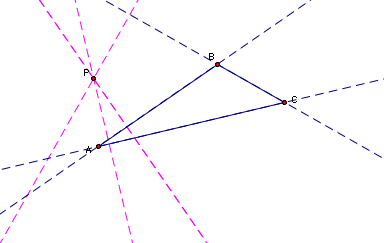
Construct the points of intersection E, F, and G.

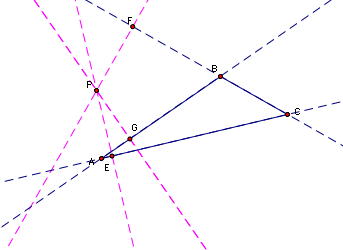
Construct the triangle EFG--this is the pedal triangle.

 

 

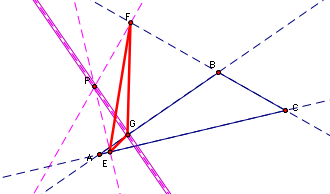
Click here for a GSP tool to construct a pedal triangle to a given triangle where P is any point in the plane.

Let's explore what happens when P lies on the circumcircle of the original triangle ABC. Based on this construction, I conjecture that when the point P is on the the circumcircle of the original triangle ABC, that the pedal triangle is a line (Simson Line) rather than an actual triangle.

 

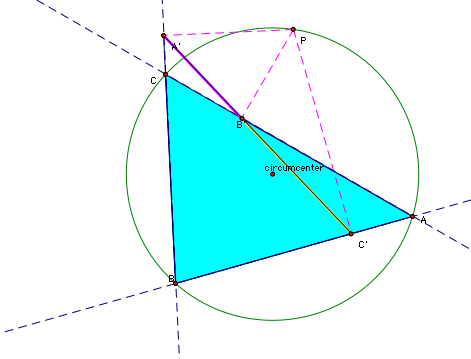
Proof:

Consider triangle AB'C', PC' is perpendicular to AC' because C' lies on line AB. PB' is perpendicular to AB' because AB' lies on AC.

Because angle PC'A is 90 degrees and angle AB'P is 90 degrees, we can construct a circle through points A, B', P, and C' so that AP is a diameter of the circle. This circle will also be the circumcircle of triangle. AB'C' and P is on the circumcirle of AB'C'. This also means that AB'C'P is a cyclic quadrilateral.

By similar arguments, we can show that P is on the circumcircle of triangles A'BC' and A'B'C and thus that A'BC'P and A'B'CP are cyclic quadrilaterals.

By the original construction, the quadrilateral ABCP is a cyclic quadrilateral because the vertices lie on a common circle.

If we show that angle A'B'C equals angle C'B'A' then the points A', C', and B' ar collinear (because by construction A, C, and B' are collinear and we now have vertical angles).

 

The measure of angle A'PC' + the measure of angle A'B C' = 180 degrees. (Opposite angles in cyclic quadrilaterals sum to 180 degrees)

the measure of angle A'BC' = the measure of angle CBA because they are the same angle.

We can substitute to get:

<A'PC' + <CBA = 180 degrees.

<CBA + < CPA = 180 degrees (opposite angles in a cyclic quadrilateral)

Subtracting these two equations we get

<A'PC' - <CPA = 0

or

<A'PC' = <CPA

Now subtract angle CPB' from each side.

<A'PC' - < CPC' = <CPA - <CPC'

we get

<A'PC = <C'PA

Since C'B'PA is cyclic quadrilateral, < C'PA = <C'B'A (inscribed circles cutting off the same arc)

Similarly, A'PB'C is a cyclic quadrilateral and <A'PC = A'B'C.

Combining the bold equalities, we have <A'B'C = <C'B'A and the points A', B', and C' are collinear.