Exploring Parametric Equations

By Mary Negley

For this exploration I will look at and , where and and are different values. First I will look at the case when .

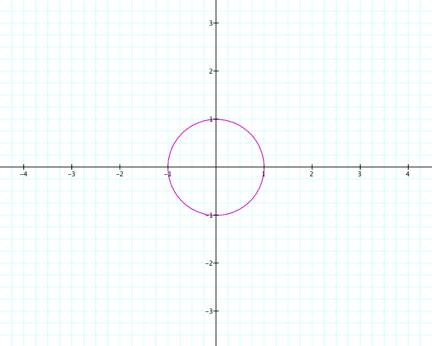
When , a circle of radius 1, centered at the origin, is formed.

How about if , but every other condition remains unchanged? Will the graph change?

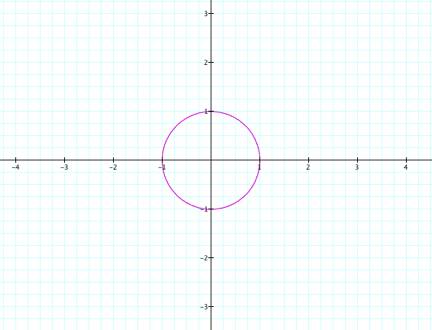
Clearly, the graph is unchanged. Through own exploration, one may easily find that if and , the graph will be identical to the two previous graphs.

Now let’s explore when . In this example, let and .

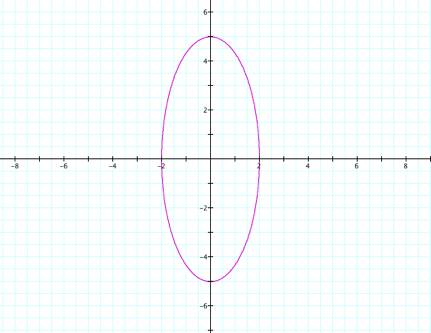
The graph is now an ellipse, instead of a circle. It is longer vertically than it is horizontally, and it is still centered at the origin, but it crosses the x-axis at -2 and 2 and it crosses the y-axis at -5 and 5. Notice that in this example, and , and the positive and negative values of those two numbers are also the points where the graph crosses the axes. My prediction is that the graph will always cross the x-axis at and the y-axis at. Now, let’s see what happens if I graph the same parametric equations only this time and . If my prediction is correct, then the new graph should be an ellipse that is longer horizontally than it is vertically and centered at the origin. Moreover, the graph should cross the x-axis atand the y-axis at.

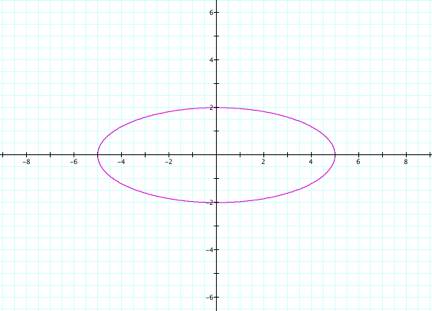
I was correct.

From looking at the previous four graphs, one would assume that if , then the graph would be longer vertically than horizontally, if , then the graph would be longer horizontally than vertically, and if , then the graph would be a circle. Let’s try a few more cases testing those assumptions.

First we will study when . First let’s look at when and .

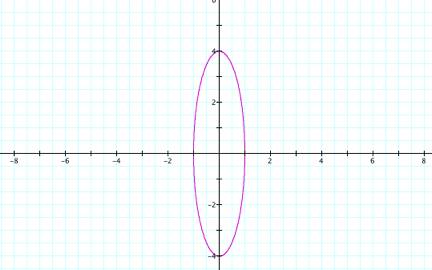
This graph is an ellipse that is longer horizontally than it is vertically. Now let’s look at when and .

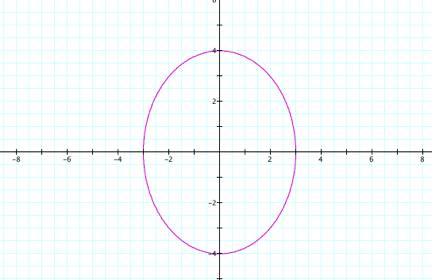
Again, this is an ellipse, which is longer vertically than it is horizontally. Now let’s look at the case when . This time let’s look at when and .

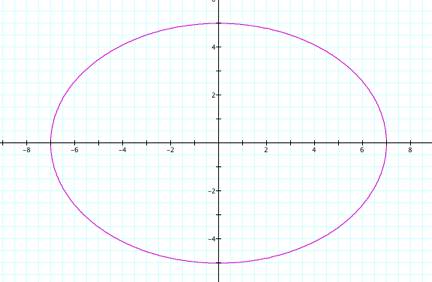
Notice that this time we have an ellipse that is longer horizontally than it is vertically. Now let’s try when and .

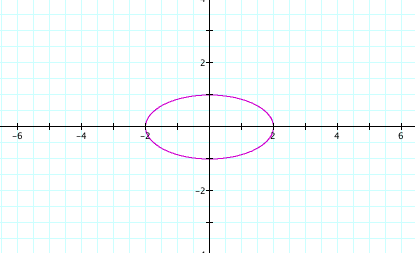
Again, we have an ellipse, which is longer horizontally than it is vertically.

Now I will investigate the graphs of the following equations:

for

where h is any real number.

First I want to look at the case when , and .

This graph appears to be similar to the ellipse from two examples ago, but it is skinnier and it has been rotated 45 degrees counter-clockwise about the origin. Let’s see what happens when .

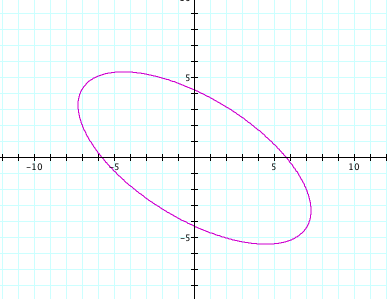
This appears to be the same ellipse as the previous example only this time it is rotated clockwise instead of counter-clockwise. What happens if ?

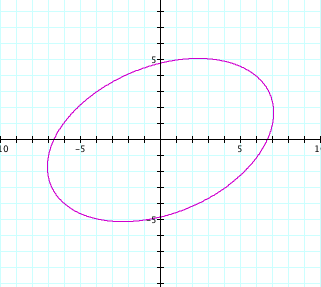
This appears to be an ellipse that it rotated 45 degrees counter-clockwise and it is wider than the previous ellipse. If , I would suggest that it would be an ellipse identical to the previous one, only it is rotated 45 degrees clockwise.

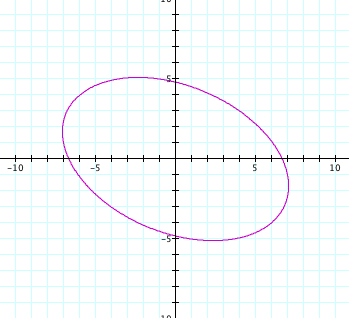
My suggestion was correct.

Return