Explorations with Binomials
By Mary Negley
In this exploration, we will look at the
binomial
and how one may manipulate it.
First let's graph it.
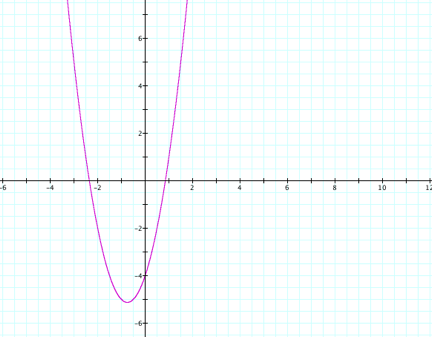
Notice how the vertex is located in the third
quadrant and it appears to be close to 
. In order to find the actual location of the vertex, we may
take the derivative of the binomial and set it equal to 0.
So we find that 
. Setting the derivative equal to 0, we get:
We then use the value that we found for x to find the y value of the vertex.
So the vertex is located at
.
For the next part, we need to replace each x in the binomial by
. So the
binomial we get is 
. Then we graph
this new binomial on the same axes as the original binomial and we get:
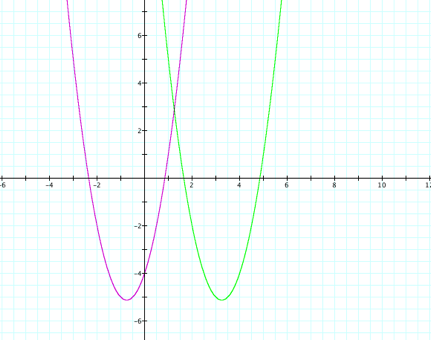
Notice how the new graph appears to be
translated 4 units to the right.
By solving for the derivative again, setting it equal to zero, and then
using the x-value that we get to
find the y-value, we find that the
vertex of the new graph is 
. Notice that
the y-value stayed the same, but
the x-value increased by 4 units,
which shows that the graph was translated 4 units to the right.
Next we must change the equation to move the vertex
of the graph into the second quadrant.
The new equation becomes
and it is graphed below.
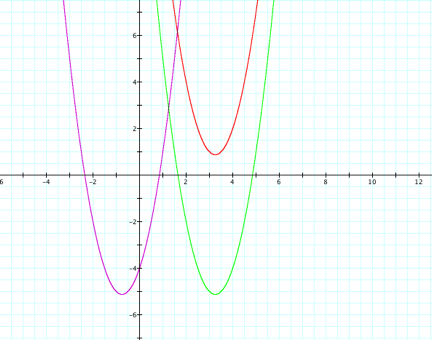
Using the same method as before to find the
vertex, I find that the vertex is 
.
Finally we need to change the equation to
produce a graph, which is concave down and shares the same vertex as the
previous equation. After several
attempts, I find that the new equation is 
and it is
graphed below.
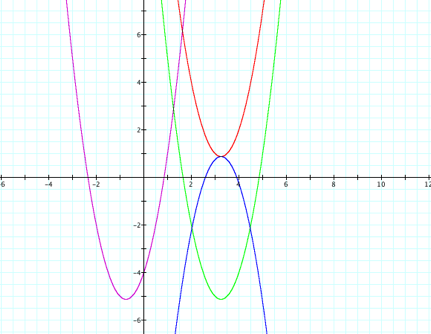
To confirm that the new graph shares the same
vertex as the previous graph, I use the same method as before. I find that the vertex of the new graph
is 
. We see that
the vertices are indeed the same and so I have found a graph that is concave
down and shares the same vertex as the previous graph.