Exploring

By Mary Negley

In this exploration, I will look at graphs of the quadratic for various values of b and discover a relationship among the vertices. Below are the graphs of , where b is equal to integers ranging from -3 to 3, on one grid.

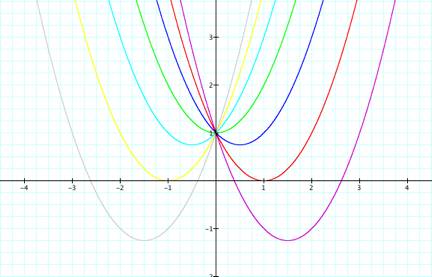
When , the graph is fuschia. When , the graph is red. When , the graph is blue. When , the graph is green. When , the graph is light blue. When , the graph is yellow. When , the graph is gray.

Notice that when and , the graphs cross the x-axis at exactly two places, when and , the graphs touch the x-axis at precisely one place, and for the other values of x, the graphs do not touch the x-axis.

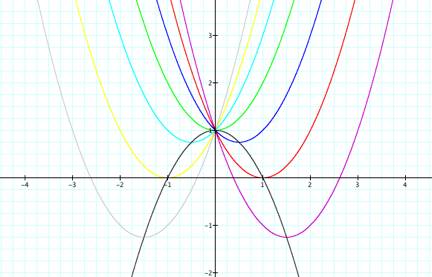
A conjecture is that the vertices of the above quadratics all lie along the quadratic . Below is a picture of the quadratic with the previous quadratics and it appears that the conjecture is correct. To be more certain, I will calculate the vertices of the quadratics and determine whether they lie along the quadratic .

To find the vertex of a parabola, I can calculate the derivative of the quadratic, set that derivative equal to zero, solve for x and then plug that x-value into the original equation to find the corresponding y-value. I will then have the vertex.

First I will find the vertex of .

1. Find the derivative.

2. Set it equal to zero and solve for x.

3. Plug that value into the original equation and solve for y.

So the value of the vertex is .

Likewise, using the method above you can get that the vertices are:

b-value	Vertex
-3
-2
-1
0
1
2
3

Notice that the difference between the y-value of the first vertex in the chart and the y-value of the second vertex is . The difference between the second and the third is . The difference between the third and the fourth is and the difference between the fourth and the fifth is . The difference between the fifth and the sixth is . Finally, the difference between the fifth and the sixth is . Since the differences are not constant, I know that the relationship among the vertices is not linear. Taking the differences one more time, I find that the difference is a constant , so the relationship is quadratic. I already know the value of the y-intercept because one of the vertices is , which must be the y-intercept. To find the rate of change of the quadratic, I take the points and and I find that the slope is -1. So the quadratic must be and thus, our conjecture is correct.

Return