
Tangent Circle Construction
By Mary
Negley
For
this assignment, I constructed tangent circles in a variety of situations. For my first case, I looked at the
following problem:
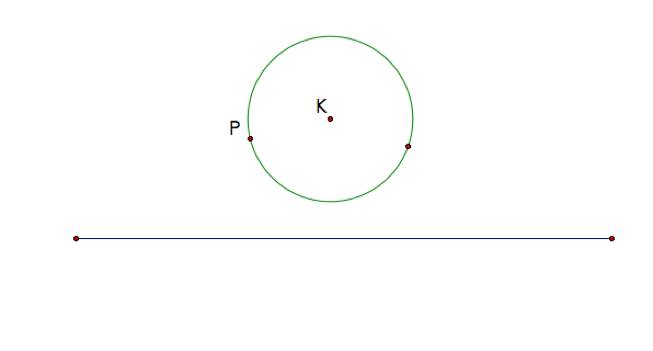
Given
a line and a circle with center K.
Take an arbitrary point P on the circle.
Construct two circles tangent to the given circle at P and tangent to the line.
In order to find the solution, I needed to think
through the properties of tangent circles. Below is a sketch of the line and circle with center K.
We
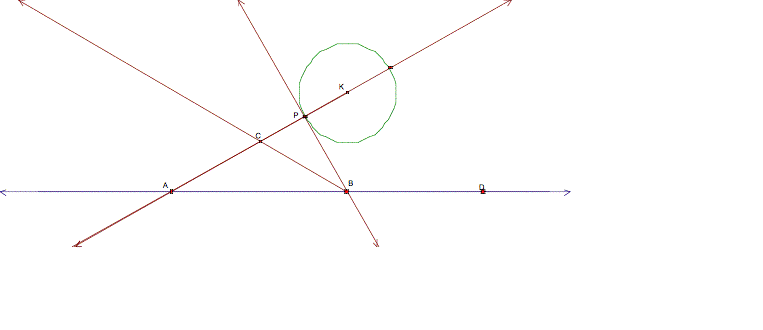
know that the circle, which is tangent to the circle with center K, will have its point of tangency with the circle at P because that is given. So the first step is to create a right angle at that
point. We do this by extending the
radius of the circle into a line at P
and creating a line perpendicular to the line through K and P at P.

To
construct a tangent circle, I bisected the angle ABP and I found the intersection of the angle bisector and
the line through P and K. I
labeled this intersection point C.
Then I constructed a circle centered at C with the radius CP.
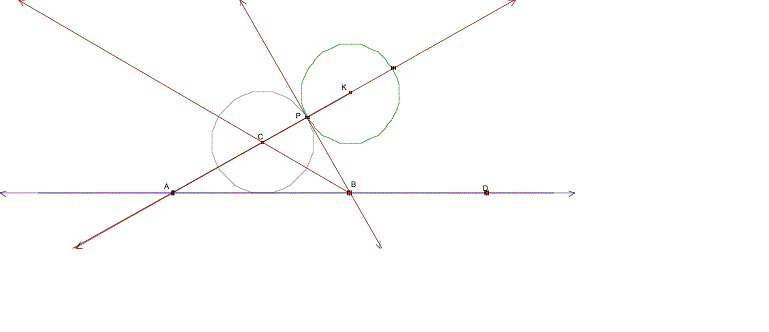
Then, to construct the other tangent circle, I
bisected the angle PBD and found
the intersection of the angle bisector and the line through P and K. I labeled the intersection point E.
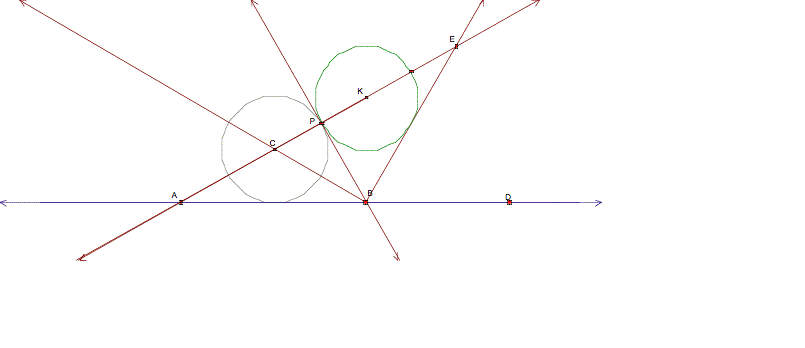
I then constructed a circle centered at E with the radius of BE.

Thus, I have constructed two circles tangent to the
given circle at P and tangent to
the line.
Suppose I wanted to construct a circle tangent to a
larger circle with a smaller circle inside it. See below for a possible sketch.
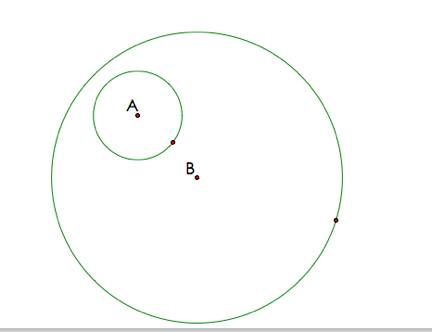
Using the strategy that I implemented above, I created
a line through A and B and found the intersections of the line with the
circles and labeled those.

An easy tangent circle to construct is the one tangent
to the larger circle at C and
tangent to the smaller circle at D. To construct that tangent circle, I
find the midpoint of the segment CD
and create a circle centered at that midpoint with the radius ![]() .
.

Another tangent circle may be formed by finding the
other point of intersection of the line and the smaller circle, labeling this
point E and finding the midpoint
of CE and creating a circle
centered at the midpoint with the radius![]() .
.

A script of those two constructions may be found here.