
Altitudes and Orthocenters
By Mary Negley
For this assignment, I will explore the following
problem:
Given
triangle ABC. Construct the
Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B,
and C, respectively. Prove:
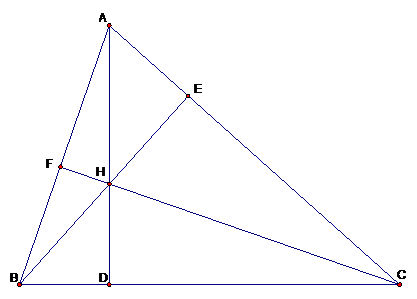
(1)![]() and (2)
and (2) ![]() .
.
Below is a GSP sketch of the triangle
ABC.
First I will prove the first statement. Notice the triangle ABC may be
split into three smaller triangles: Triangle HBC, Triangle HAC,
and Triangle HAB. I will use
the areas of the triangles to prove this statement. Remember that the definition of an
orthocenter is the intersection of the three altitudes of the triangle. The altitudes may also be known as the
heights of the triangle.
We know that:
Area
of Triangle ABC = the Sum of the Areas of the Smaller Triangles.
Area
of Triangle ABC = ![]()
If you divide both sides by the Area of Triangle ABC, you get:
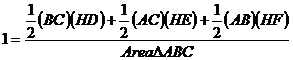
The Area of Triangle ABC can be written in three different ways:![]() ,
, ![]() , or
, or ![]() . I am going to use
all three in the equation.
. I am going to use
all three in the equation.
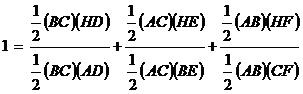
After simplifying, I get![]() . Hence, I have proved
the first part.
. Hence, I have proved
the first part.
Now I will show that![]() .
.
![]()
![]()
Notice that in first part, I showed that![]() . I use that fact
here.
. I use that fact
here.
![]() .
.
Thus, I have shown that![]() .
.
A couple questions that may arise are “Does this only hold for acute
triangles? What
about if the triangle is obtuse?”
Below is a GSP sketch of an obtuse triangle.

Notice that the orthocenter occurs outside of the triangle. In order to calculate the areas, I need
to extend the legs of the triangle.
Below is a new sketch.
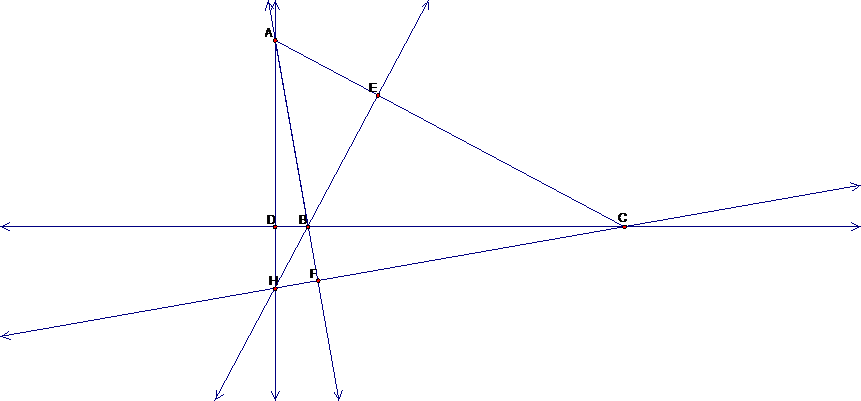
Now I want to see if (1)![]() and (2)
and (2) ![]() . Looking at the
triangle and calculating the lengths, I get:
. Looking at the
triangle and calculating the lengths, I get:
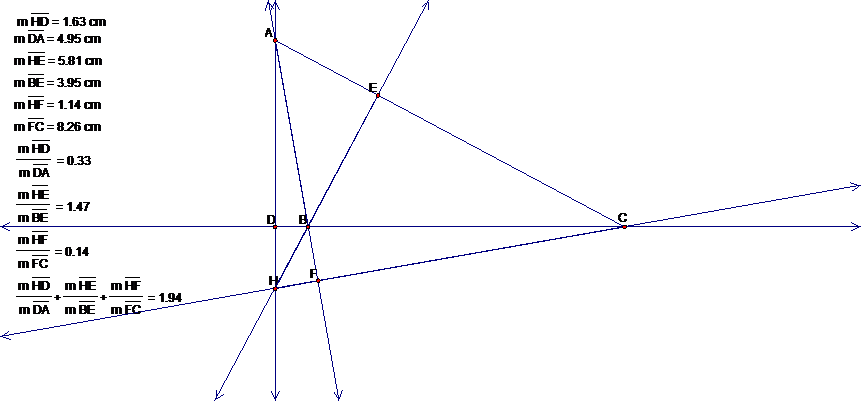
So the first statement is untrue and likewise, the second statement is
false.
By looking at the graph, one can tell that the first statement will be
false because ![]() since
since![]() ,
, ![]() since
since ![]() and
and ![]() since
since ![]() and
and ![]() . So since one
part of the sum is greater than 1 and the other two parts are greater than 0,
the whole sum must be greater than 1, so the first statement is false. Because the first statement is false and
we use it to prove the second statement, it also must be false.
. So since one
part of the sum is greater than 1 and the other two parts are greater than 0,
the whole sum must be greater than 1, so the first statement is false. Because the first statement is false and
we use it to prove the second statement, it also must be false.
So (1)![]() and (2)
and (2) ![]() are not true when
Triangle ABC is an obtuse triangle.
are not true when
Triangle ABC is an obtuse triangle.