
Pedal Triangles Exploration
By Mary
Negley
For this assignment I will explore pedal triangles and
demonstrate what happens when the pedal point is animated around different
paths. First things first! What is a pedal triangle?
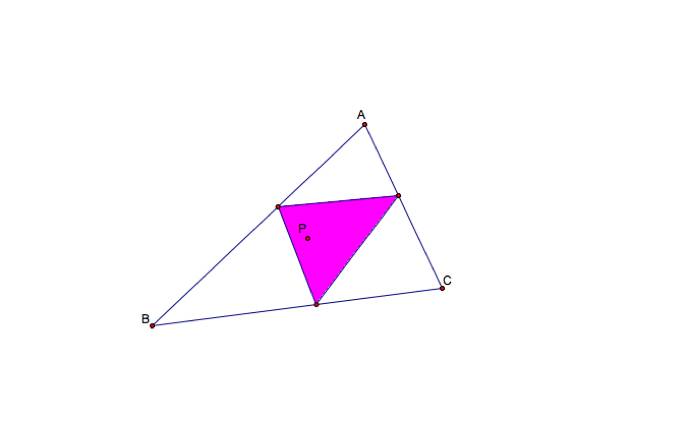
A
pedal triangle is created by constructing lines from a point P, which is anywhere in the plane, perpendicular to the
sides of a triangle ABC. The intersections of the lines with the
sides of the original triangle are the vertices of the pedal triangle. Click here for a GSP sketch, where you
will be able to move around point P
and see many possible pedal triangles.
The first problem, with which I am faced, is the
following:
Animate the pedal point P about the incircle of ABC. Trace
the loci of the midpoints of the sides. What curves result? Repeat if ABC is
a right triangle.
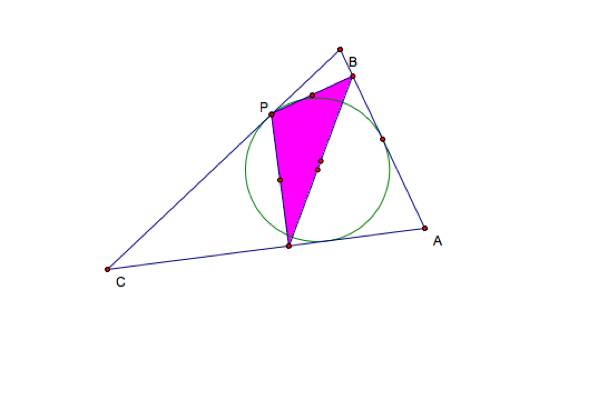
To find the answer, I must first know what an incircle
is. An incircle is, by definition,
the circle that is tangent to all three sides of a triangle and its center is
the incenter of the triangle, which is the concurrence point of the angle
bisectors. Below is a sketch of
the triangle with its incircle.
Now I will animate P about the incircle and trace the midpoints of the
sides of the pedal triangle. Click
here
for GSP sketch with animation.
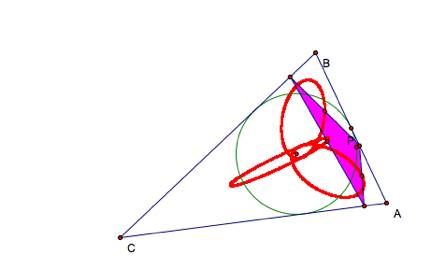
It appears that ellipses result.
What happens if Triangle ABC is a right triangle?
Click
here
for GSP sketch with animation.
The
following result occurs:
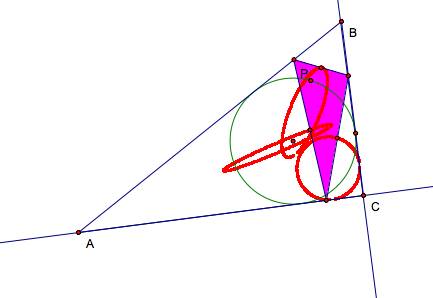
The traces still create two ellipses, but a circle is
also created.
My next problem is as follows:
Construct an excircle of triangle ABC. Animate
the pedal point P about the
excircle and trace the loci of the midpoints of the sides of the pedal
triangle. What curves result? Look at the angle bisectors through the
center of the excircle. How are
the loci positioned with respect to the angle bisectors?
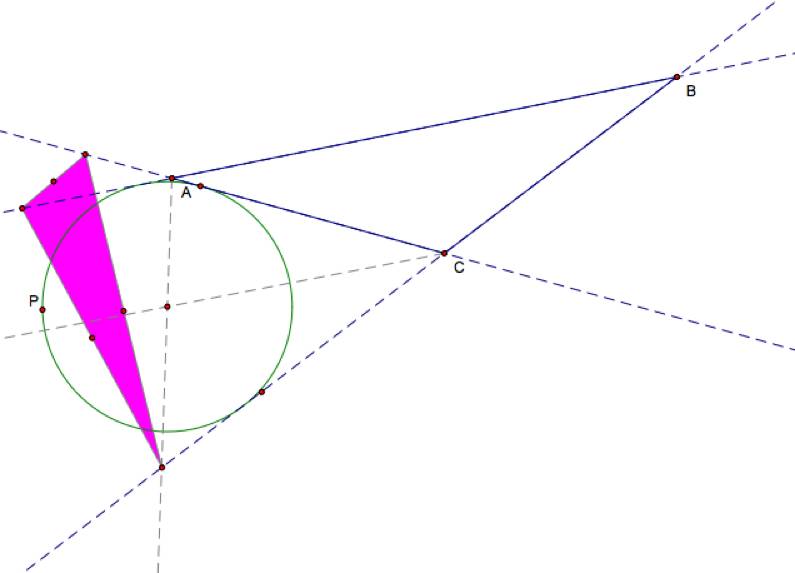
This time I need to know what an excircle is. An excircle is, by definition, centered
at the intersection of the external angle bisectors of two vertices and tangent
to the side between those two vertices and also tangent to the extension of the
other two sides. An example is
given below.

Now I will pick a random point on the excircle to be
the P and I will create a pedal
triangle based on that point.
Like in the last problem, I will trace the midpoints
of the sides as P goes along the
circle. Click here
for a GSP sketch with animation.
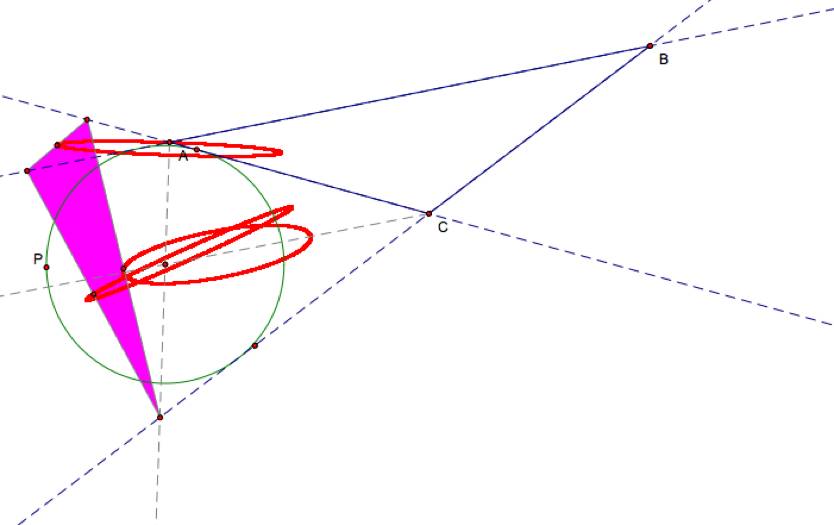
Like last time it appeared to make ellipses. To answer the second part of the
problem (Look at the angle bisectors through the center of the excircle. How are the loci positioned with respect
to the angle bisectors?), I need to show the angle bisectors again.

Notice that the intersection of the exterior angle
bisectors is surrounded by two of the ellipses and the other ellipse contains
the part of an exterior angle bisector.