Bouncing Barney

By Mary Negley

For this assignment, I will explore the following problem:

Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

To better understand this problem, I constructed the following GSP sketch.

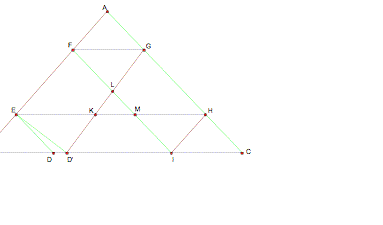
I want to assume that, so. First I will identify all the parallelograms in the figure. By construction, the following quadrilaterals are parallelograms: AFIH, GFIC, EDCH, EBIH, AFLG, GFMH, and GFEK.

By definition of parallelogram, opposite sides of a parallelogram are not only parallel; they are also equal. So the following congruent segment pairs occur:, , , and .

Now I want to focus on the parallelogram GFIC.

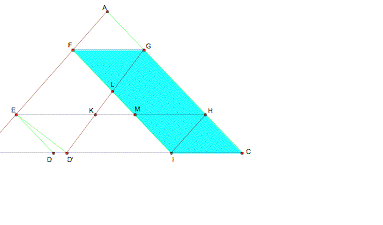
It is a parallelogram by construction and by definition and . Notice that (1)and (2). By construction, GLIH is also a parallelogram and by definition, (3)and (4) .

So we have

By (1) and (2)

By (4), we can substitute GH for LI and we get

Subtracting GH from both sides yields

In our congruent segment pairs above, we saw that and . Now that we know that, we can substitute FL for HC in the second congruent segment pair, so we get. So we see that and. Thus, , which is a contradiction, so our assumption must be false. Therefore, and Barney started at the same place that he ended.

Another question that I can answer is given above: How many times will Barney reach a wall before returning to his starting point? In my GSP sketch, it appears that he reaches five walls before returning to his starting point (or six, if one counts the wall that contains his starting/ending point). Through exploration with the GSP sketch given here, one sees that this is the case unless Barney starts at one of the vertices or the midpoint. If he starts at one of the vertices, then he walks along the walls the whole time, so he either does not reach a wall at all or always reaches a wall, depending on how one looks at it. However, if he starts at the midpoint then the starting/ending point is on the third wall that he meets. What is the mathematical reason behind that?

Below is a sketch of the situation where Barney starts at the midpoint.

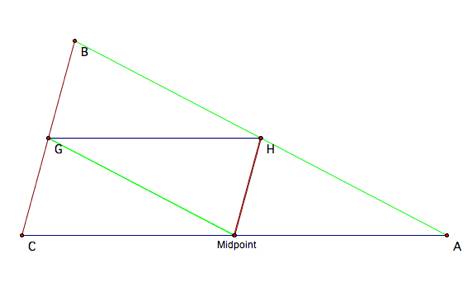
Since we know the midpoint of AC, . Since GCMidpointH was constructed to be a parallelogram, . Since BGMidpointH was constructed to be another parallelogram, . By transitivity, since and , . So G is the midpoint of BC. By a similar argument, H is the midpoint of AB. So we know that Barney reaches a wall at each of the three midpoints of the sides of the triangle. Notice that the triangle formed by Barney’s path is by definition a medial triangle. Every triangle has a medial triangle, so it makes sense that Barney’s path would be along the medial triangle. So that must be why he reaches three walls when he starts at the midpoint.

Return